知识表示
知识表示
把有关信息关联在一起所形成的信息结构称为知识。把有关信息关联在一起所形成的信息结构称为知识。
知识的性质
相对正确性:1+1=10 在不同的进制下有不同的正确性;
不确定性:知识并不总是只有“真”和“假”两种状态。以下原因导致了这条性质:
① 随机性:我有八成的把握打中目标。
② 模糊性:高个子适合于打篮球。
③ 不完全性:莲花清瘟对新冠病毒有一定功效。
④ 经验性:土干了就给花浇水。
可表示与可利用性
知识表示的分类
| 分类方式 | 分类 |
|---|---|
| 形成 | 知识由概念、命题、公理、定理、规则和方法组成 |
| 层次 | 表层知识、深层知识 |
| 确定性程度 | 确定性知识、不确定性知识 |
| 等级 | 元知识、非元知识 |
| 作用 | 陈述性知识、过程性知识 |
过程性知识表示
过程性知识一般是表示如何做的知识,是有关系统变化、问题求解过程的操作、演算和行为的知识。 这种知识一般隐含在面向过程程序中,机器无法从程序的编码中抽取出知识。
这种知识的描述表示控制规则和控制结构的知识,给出一些客观规律,告诉怎么做。
例如矩阵求逆程序,程序中描述了矩阵的逆和求解方法的知识。
陈述式知识表示
描述系统的状态、环境和条件,以及问题的概念、定义和事实。
一阶谓词逻辑
命题
非真即假,陈述句,唯一的真值。
如果满足上述条件而暂时无法确定真值也算,明天是晴天、存在外星人都是命题。
谓词
例:
老张是老师:
5>3:
小李的妹妹与小张的哥哥结婚:
其中
谓词公式
连接词
例:
如果Jones造了一个传感器,且这个传感器不能用,那么他要么晚上修理要么第二天把它交给工程师:
量词
例:
某个工程师可以操作车床:
每个雇员都有一个经理:
有一个人是所有雇员的经理:
每个人都有喜欢的人:
有的人被所有人喜欢:
兼爱:
理想社会:
谓词公式
上边几种符号有限组合就是谓词公式。
优先级从高到低:
量词辖域
换名规则
自由变元随便换(不能用约束变元的名),约束变元统一换:
谓词公式的性质
解释
一个解释就是命题公式中所有变元的一组真值。一个解释能给公式确定唯一一个真值。
永真性
任何解释下公式都为真就是永真。
可满足性
至少一个解释下为真就是可满足。
不可满足性
任何一个解释下都不为真就是不可满足,即永假。
等价性(等价式)
交换律
结合律
分配律
De Morgen律
拆括号内部全取反,与或互换。
双重否定律
吸收律
补余(否定)律
连接词 化归律
用来处理箭头
逆否律
量词转换律
不存在
量词分配律
谓词公式的永真蕴涵
如果
假言推理
由
拒取式
假言三段论
构造性两难
全称固化
存在固化
反证法
后半部分的意思就是前边那些P都满足时Q不可能是假的。
置换与合一
在基于谓词的推理过程中,会出现谓词名相同但其个体不同的情况,此时不能直接进行匹配的,需要先进行置换。在推理过程中,寻找项与项之间的置换,使不同谓词表达式一致的过程叫做合一的过程。
置换
置换是用置换项替换变量。置换项可以是常量、函数或变量。
定义
置换是形如
例:
规则
只能用常量、函数或变量置换变量,不能用变量置换常量和函数,不能用常量和函数置换不同的常量和函数。
不能循环置换,如
合一
定义
设公式集
例:
则它的一个合一是
因为:
对于
对于
一般来说一个公式集的合一不唯一。
最一般合一
定义
设
一个公式集的任一合一都可由最一般合一和一个置换的合成置换得到。
最一般合一是唯一的。
例:
引入置换
最一般合一的求法
求
步骤:
先找出第一个不一致集
之后找第二个不一致集
最后一个不一致集
则
产生式
产生式
确定性规则知识
不确定性规则知识
确定性事实性知识
例:
老李40岁:
老李和老王是朋友:
不确定性事实性知识
例:
老李很有可能40岁:
老李和老王不太会是朋友:
蕴含式与产生式
产生式可以表示不确定知识,并且包括操作、规则、变换、算子、函数等,这些蕴含式都做不到。
产生式表示法的特点
产生式易于表示,且知识单元间相互独立,易于建立知识库;
推理方式单纯,适于模拟强数据驱动特点的智能行为;
知识库与推理机相分离。这种结构易于修改知识库;
易于对系统的推理路径作出解释。
产生式系统

或者:
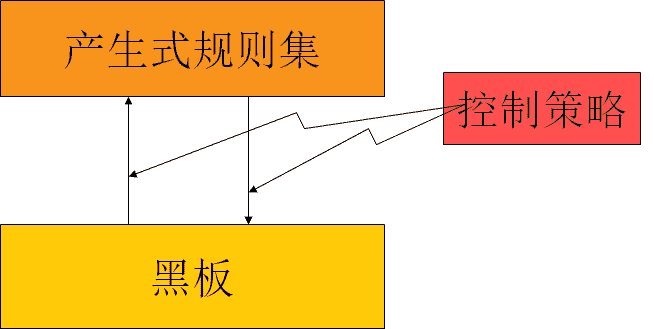
推理步骤
① 用黑板(知识库)中的事实与可用规则集中所有规则的前件进行匹配,得到匹配的规则集合;
② 从匹配规则集合中选择一条规则作为使用规则;
③ 执行使用规则,将该使用规则后件的执行结果送入黑板;并将已执行规则从可用规则集中删除;
④ 重复这个过程,直到达到目标或者无可匹配规则为止。
规则库
r1: IF 该三角形有两边相等 THEN 该三角形是等腰三角形
r2: IF 该三角形两边相等 AND 第三边也相等 THEN 该三角形是等边三角形
r3: IF 该三角形有一个钝角 THEN 该三角形是钝角三角形
r4: IF 该三角形有一个直角 THEN 该三角形是直角三角形
r5: IF 该三角形不存在钝角或直角 THEN 该三角形是锐角三角形
r6: IF 该三角形是等腰三角形 AND 有一个钝角 THEN 该三角形是等腰钝角三角形
r7: IF 该三角形是等腰三角形 AND 不存在钝角或直角 THEN 该三角形是等腰锐角三角形
r8: IF 该三角形是等腰三角形 AND 有一个直角 THEN 该三角形是等腰直角三角形推理机构工作过程
取出r1,符合
此时
之后的条目均不符合,直到:取出r8,符合
特点:
自然性、模块性、有效性、清晰性;效率不高、不能表示有结构的知识。
框架表示法

框架表示法类似面向对象,通过属性组合来描述一件事。
例如产生式规则:如果头疼且发烧就是感冒,框架表示为:
框架名: <诊断1>
前提:条件1 头疼
条件2 发烧
结论:感冒结构
一个框架由若干个“槽”组成,一个槽又可划分为若干个“侧面”。一个槽用于描述所论对象某一方面的属性,一个侧面用于描述相应属性的一个方面。
<框架名>
槽名1: 侧面名1 值1,值2,…,值p1
侧面名2 值1,值2,…,值p2
…
侧面名m1 值1,值2,…,值pm1
槽名2: 侧面名1 值1,值2,…,值q1
侧面名2 值1,值2,…,值q2
…
侧面名m2 值1,值2,…,值qm2
…
槽名n: 侧面名1 值1,值2,…,值r1
侧面名2 值1,值2,…,值r2
…
侧面名mn 值1,值2,…,值rmn
约束: 约束条件1
约束条件2
…
约束条件n例如:
框架名:<教师>
姓名:单位(姓、名)
年龄:单位(岁)
性别:范围(男、女)
缺省:男
职称:范围(教授、副教授、讲师、助教)
缺省:讲师
部门:单位(系,教研室)
住址:<住址框架>
工资:<工资框架>
开始工作时间:单位(年、月)
截止时间:单位(年、月)
缺省:现在框架间的联系
框架中的槽值或侧面值都可以是另外一个框架,也就是说框架之中还可以包含框架。这就在框架之间建立起了联系。这种联系是一种包含关系,称为横向联系。
框架之间还可以有继承关系,称为纵向联系。框架中可以有“继承”槽,指明上下关系。
这里可以参考·面向对象思想中的类理解。
特点:
结构性、继承性、自然性。
网络结构表示法
Petri网

表示方式
基本的Petri网可用三元组
P(Place)表示位置集合,一般表示事物属性或状态;
T(Transition)表示转换集合,表示从一种状态转变为另一种状态;
F 表示有向弧集合,用于指明转换的方向,有向弧只能存在于P和T或者T和P之间。
在并发系统中,一个位置可以拥有多个令牌(Token),用于进行并发控制。
特点
便于描述系统状态的变化以及对系统动态特性进行分析;
可以在不同层次上变换描述,而不必注意细节及相应的物理表示。
语义网络
结构
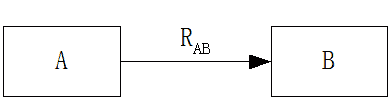
语义网络是通过概念及其语义关系来表达知识的一种网络图。
从图论的观点看,它就是一个“带标识的有向图”。有向图的节点表示各种事物、概念、情况、属性、状态动作等等。弧表示各种语义联系,也称为联想弧。
例

边只用来表示联系,单拿出一条边来是没有意义的,一条边和它两端的东西结合才有实际意义。
特点
结构性,联想性,直观性,非严格性,处理复杂性。
其他表示法
脚本表示法:脚本与框架类似,由一组槽组成,用来表示特定领域内一些事件的发生序列。
过程表示法:这种表示法认为知识主要是过程性的。其表示方法应将知识及如何使用这些知识的控制性策略均表述为求解问题的过程;过程性表示方法着重于对知识的利用,它把与问题有关的知识以及如何运用这些知识求解问题的控制策略都表述为一个或多个求解问题的过程。
知识获取与管理
任务
需要获取知识,建立起健全、完善、有效的知识库,以满足求解领域问题的需要。
知识获取方式
非自动知识获取

自动知识获取

知识管理
任务
具体地、物理地组建知识库,保存知识;在知识库中安排具体的知识;实现知识的增删改查;记录变更;保证知识库的安全。
组建知识库的原则
具有相对独立性;便于搜索;便于运维(增删改查);便于存储多种模式表示的知识。
功能
重组知识库;记录系统运行实例;记录系统运行历史;记录知识库发展史;知识库的安全保密。
本体论
机制理论
面向形式的研究,用于处理逻辑与知识表示。
内容理论
用于处理知识的内容。
本体论
面向的是“内容”,本体是关于概念化的明确表达。本体论研究特定领域知识的对象分类、对象属性和对象间的关系,为描述领域知识提供术语。
本体是对某一概念化所做的一种显式的解释说明。
可以通过定义一套知识表示的专门术语来定义一个本体。以人们可以理解的术语来描述领域世界的实体、对象、关系以及过程等,并通过形式化的公理来限制和规范这些术语的解释和使用。
我估计这个不大会考,更多的信息详见这篇文章。
知识图谱
知识图谱是一种揭示实体之间关系的语义网络,可以对现实世界的事物及其相互关系进行形式化地描述。
表示
一般用三元组表示:
其中:G是知识图谱,E是知识库中的实体集合,R是知识库中的关系集合,S代表知识库中的三元组集合。
三元组的主要形式
其中:
实体是知识图谱中的基本元素,不同实体间存在不同关系。
概念主要指集合、类别、对象类型、事物的种类等。
属性指对象可能具有的属性、特征、特性、特点以及参数等。
属性值是指对象指定属性的值。
属性-属性值对可用来刻画实体的内在特性。
关系可用来连接两个实体,刻画它们之间的关联。
特点
广泛认可,但在计算效率、数据稀疏性等面临诸多问题。
把知识分布式表示,用一个综合向量来表示实体对象的语义信息,模仿人脑工作的表示机制,将实体语义信息表示为稠密低维实值向量,进而在低维实数空间中高效计算实体、关系及其之间的复杂语义关联。
图谱结构
逻辑上可分为数据层和模式层。数据层主要由一系列事实组成,知识以事实为单位进行存储;模式层构建在数据层之上,主要是通过本体库来规范数据层的一系列事实表达。
构建方式
主要有自顶向下和自底向上两种方式。自顶向下是指先为知识图谱定义好本体与数据模式,再将实体加入到知识库;自底向上是指从一些开放链接数据中提取出实体,选择其中置信度较高的加入到知识库,然后再构建顶层的本体模式。
i
自顶向下是先定义后加库;自底向上是先建库再定义。
知识抽取
分为知识抽取,实体抽取,关系抽取和属性抽取。
知识融合
包括实体对齐、知识加工、知识更新等内容:
实体对齐,也称为实体匹配,用于消除异构数据中实体冲突、指向不明等不一致性问题;
知识加工,从层次上形成一个大规模的知识体系,统一对知识进行管理;
知识更新,不断迭代并扩展新知识。
知识图谱的推理
分为基于逻辑、图的推理。
基于知识的系统
知识系统是一类具有专门知识和经验的计算机系统,并通过对人类知识和问题求解过程的建模,采用知识表示和知识推理技术来模拟通常由人类解决的复杂问题。
基于知识的系统以知识库和推理机为核心。知识系统把知识与系统其它部分分离开,并且知识系统强调知识而不是方法。
知识工程
是建造知识系统的过程。包括:知识获取、知识表示、设计知识库和推理机、用适当的语言实现系统。
知识系统的特点
启发性、灵活性(一般知识系统的体系结构都采用了知识库与推理机分离的原则)、交互性(知识系统一般采用交互方式进行人机通信)、实用性(知识系统是根据具体应用领域的问题开发的,针对性强)、易推广。
专家系统
是具有专门领域知识,能够像人类专家一样解决一些特定领域问题的一类知识系统:
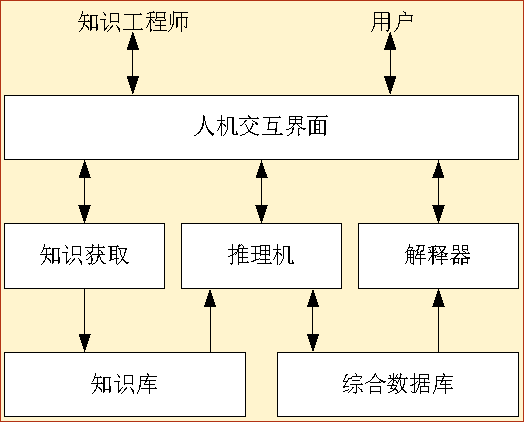
问答系统(RAG)
是指以自然语言(文本或者语音)提问为输入,能够自动给出相应自然语言(文本或语音)答案的一类人工智能知识系统。
