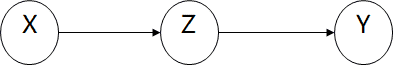不确定性推理是建立在非经典逻辑基础上的一种推理,它是对不确定性知识的运用与处理。
严格地说,所谓不确定性推理就是从不确定性的初始证据出发,通过运用不确定性的知识,最终推出具有一定程度的不确定性但却是合理或者近乎合理的结论的思维过程。
产生式规则:
是可信度,要算可信度就需要条件概率,和先验概率,。
是一系列变量的联合概率分布的图形表示;是一个表示变量之间的相互依赖关系的数据结构;是图论与概率论的结合。
贝叶斯网络图是一个有向无环图,其中图中的每个节点代表相应的变量。当有向弧由节点A指向节点B时,则称:A是B的父节点;B是A的子节点。被指到的是儿子。节点和节点之间的条件概率表就是一系列的概率值,表示了局部条件概率分布。
命题S(smoker):该患者是一个吸烟者;
命题C(coal Miner):该患者是一个煤矿矿井工人;
命题L(lung Cancer):他患了肺癌;
命题E(emphysema):他患了肺气肿。
由专家给定的假设可知,命题S对命题L和命题E有因果影响,而C对E也有因果影响。命题之间的关系可以描绘成因果关系网。每一个节点代表一个证据,每一条弧代表一条规则(假设),连接结点的弧表达了由规则给出的节点间的直接因果关系。
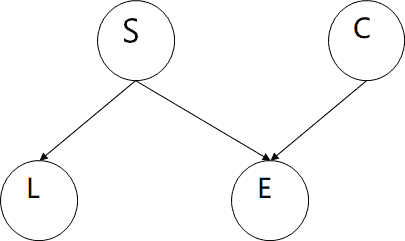
之后为各个节点指派概率,并给每个弧指定连接强度(父节点有多大可能导致子节点?):
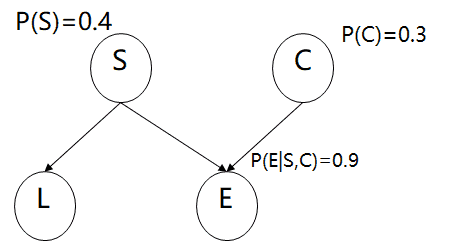
联合概率是:
如果它们相互独立:
用条件概率可以表示为:
迭代表示:
如果在给定Z的条件下,X与Y相互独立,则:,因为:
上面那张图中的联合概率密度是:
由图可知:E与L在S条件下独立(兄弟节点彼此之间没有联系),所以,另外,L与C在S条件下独立,所以,C与S独立,所以。
给定父节点的状态后,每个变量与它在图中的非继承节点在概率上是独立的。
可以根据上述方式简化联合概率密度:
对于单个变量X, Y, E:,X与Y在给定E的条件下独立可得:
对于多个变量:
如果与在给定的条件下独立,有:
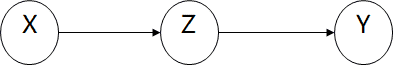
串行连接中,事件X通过事件Z影响事件Y,反之事件Y也是通过事件Z影响事件X。但是,如果原因证据Z是给定的,X并不能给Y更多的东西,或者说,从X那里得到更多的信息。
此时称,如果Z是已知的,那么通道就被阻塞,X和Y就是独立的了。则称X和Y是被Z节点D分离的,即
当Z已知时,X对Y的影响完全被Z捕捉,Z作为中介阻断了X和Y之间的直接关联。
例如:
X:是否下雨;Z:地面是否湿;Y:是否有人摔倒。
对应关系是:
如果不知道Z(是否湿),只知道X(是否下雨),那么下雨可能影响是否有人摔倒,Z和X相关。
但是如果知道了Z,即知道地面的潮湿情况,那就无需知道是否下雨即可判定是否有人摔倒的情况,因为下雨和摔倒的关联完全被Z捕捉。若地面没有湿,则摔倒与下雨无关。因此在Z被观察到时,X和Y条件独立。
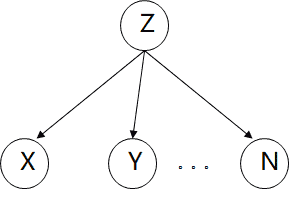
如果Z已知,那么X,Y,...条件独立(被Z D分离)。
例如:
Z:一个人的遗传基因;X:此人是否身高较高;Y:此人是否体重较大;N:此人是否智商较高。
如果Z的状态已知,那么身高体重智商等性状都可以由Z解释,它们彼此之间分离。

例如:
X:是否是高水平运动员;Y:是否接受了高质量的饮食;Z:是否身体健康。
X和Y共同影响Z,但是X和Y和他们的所有兄弟都互不影响。
设想如下情况:
X:是否有人偷了钥匙;Y:门锁是否损坏;Z:房间是否被闯入。
因果关系为:,是汇集连接。当不知道Z时,X和Y条件独立,即。
但是当Z已知时,X和Y就会互相影响。比如已知房间被闯入了,同时又知道没人偷钥匙,那门锁损坏的概率就会增加;相反也一样。
同样地,如果Z的某个后代已知(比如警报响起),也就等于已知Z,也能使X和Y关联。
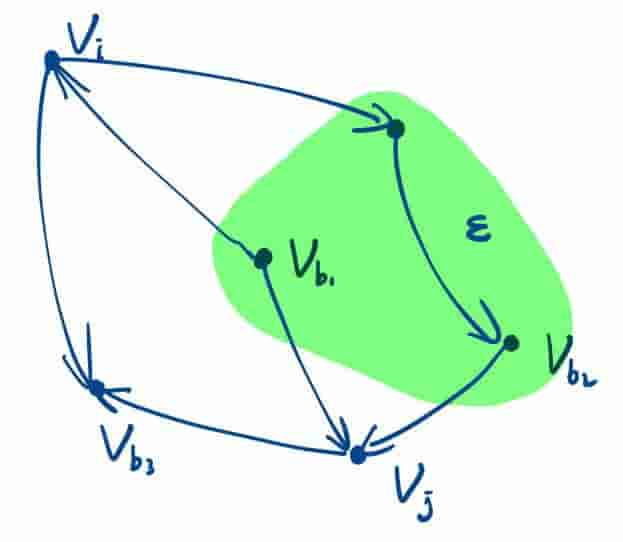
出现如图所示的三种情况就可以说阻塞了和:
① 在证据集里,两条弧都指向别人;
② 在证据集里,两条弧一个指别人一个指它自己(方向无所谓);
③ 不在证据集,它的任何后继也都不在证据集,且两条弧都指向它自己。
如果和之间所有路径被阻塞,就说明证据集可以D分离这两点;如果证据集可以D分离和,就可以说节点和独立于节点集。
因果推理:从起因到征兆(结果),起因作为证据;
诊断推理:从征兆到起因,征兆(结果)作为证据;
辩解推理:X和Y是起因,Z是两个起因的征兆。这时可以用一个起因Y解释另一个起因X。
它表示的出现概率与不出现概率之比,显然随的加大也加大。
它表示对的支持程度,取值于,由专家给出。
i
这东西为啥表示E(前提)对H(结论)的支持程度呢?
LS越大,表示E越有可能在H为真的情况下发生。比如E定义为丹炉温度高于3000K,H定义为炼出金丹,那么如果炼出金丹这件事大多发生在丹炉温度高于3000K时,就说明丹炉温度高于3000K的前提条件比较能支持炼出金丹这个结果。
它表示对的支持程度,取值范围为,也是由专家凭经验给出。
对于每个变量,其先验概率和是在没获得任何额外信息之前对变量取值的不确定程度。
假设有两个因素会导致堵车:车多和事故。
堵车的概率就是先验概率。在已知发生事故的前提下算堵车的概率,用因求果,求的是条件概率。
如果已经遇到了堵车,想算这次堵车的原因是事故的概率有多少,用果求因,就叫后验概率。
主观Bayes方法中,知识是用产生式规则表示的:
是结论的先验概率,由专家根据经验给出。
称为充分性度量,指出对的支持程度。
称为必要性度量,指出对的支持程度
和的值由领域专家给出,相当于知识的静态强度。
在主观Bayes方法中,证据的不确定性也用概率表示。
对于证据E,由用户根据观测给出,即动态强度。 由于主观给定有所困难,所以实际中可以用可信度代替。例如在PROSPECTOR中取整数:。
对应于
对应于
对应于
给定后,P计算如下:
i
证据并不一定能确定它就一定或一直能支持结论,所以要引入可信度来表示它到底能有多大概率支持。
合取取最小;析取取最大
当组合证据是多个单一证据的合取时,即
整个组合证据的确定性取决于其中最小的一个:
因为短板效应,一旦有一个无法支持结论,整个组合证据就不能支持结论。
当组合证据是多个单一证据的析取时,即
取概率最大的子证据的概率:
因为一旦有一个支持,整体就支持,除了最大概率的那个其他都没意义。
对于运算则:
主观Bayes方法推理的任务就是根据证据的条件概率及、的值,把的先验概率更新为后验概率 。
确定后验概率的方法随着证据肯定存在,肯定不存在,或者不确定而有所不同。
解释
这里的目的其实就是要写出一个公式,用表示,这个公式不确定,具体要看证据的存在性。
也就是时,来计算。
由Bayes公式:
两式相除:
几率函数
i
我一开始没看出是怎么来的,后来想起有公式:
,用它把中的 都换成 ,之后就好算了。
充分性度量的意义:
当 时, 表明由于证据的存在,增强了为真的程度。
当 时, 表明与无关。
当 时, 表明由于证据的存在,减小了为真的程度。
当 时, 表明由于证据的存在,导致为假。
时,证据肯定不存在。要计算:
由 Bayes 公式得:
两式相除:
即
必要性度量的意义:
当 时,,表明由于证据 不存在,增强了 为真的程度。
当 时,,表明 与 无关。
当 时,,表明由于证据 不存在,减小了 为真的程度。
当 时,,表明由于证据 不存在,导致 为假。
注意
由于 和 不可能同时支持 或同时反对 ,所以在一条知识中的 和 不应该出现如下情况:
在实际应用中通常取 。
时,证据不一定存在。
后验概率:
当 时,证据肯定存在,。
当 时,证据肯定不存在,。
当 时,证据与观察无关,
当 为其它值时,通过分段线性插值计算 :

EH公式:
在 PROSPECTOR 中,由于 和 遵从如下关系:
i
PROSPECTOR是一种基于贝叶斯方法的专家系统,主要用于地质勘探和资源评估。
在这里边和都是定死的,公式背下来即可。
将 代入上式得:
这就是CP公式,可以用确信值算出。
若有 条知识都支持相同的结论 ,而且每条知识的前提条件所对应的证据 都有相应的观察 与之对应(由很多组合而成),此时只要先对每条知识分别求出 ,然后运用下述公式求出 :
计算。
使用规则时,证据不确定是否发生。一定发生,由几率函数得:
由于证据肯定存在,根据肯定存在时的几率函数算出:
根据得到:
i
这个公式是用支持比的定义推出来的:
之后假设(题目中的规则要求必须发生,所以要先假设它发生的情况,之后再插值修正回来),带EH公式:
插值,由于,用后半段,
知识的静态强度 及是由领域专家给出,避免了大量的数据统计工作。和比较全面的反映了证据与结论间的因果关系,使推出的结论有较准确的确定性。
主观Bayes方法不仅给出了证据肯定存在、肯定不存在时更新后验概率的方法,还给出了证据不确定时的方法,实现了不确定性的逐级传递。
n它要求领域专家在给出知识时,同时给出先验概率及,这比较困难。
假设我们试图诊断一个病人是否患有某种疾病(例如肺炎),并且我们知道以下因素可能影响诊断结果:
症状():咳嗽(Cough)、发热(Fever)和呼吸急促(Shortness of Breath)
检验结果(T):医学影像检查异常(如胸部X光)
疾病(D):是否患有肺炎
设定每个变量的先验概率。例如,病人是否患肺炎,可以基于流行病学数据得到。
各症状的先验概率,,,也可以根据历史病例统计得出。
此时,, 为肺炎患者表现出咳嗽、发热和呼吸急促的概率。
是肺炎患者在医学影像检查中拿到异常结果的概率。
在收集数据的过程中,医生对病人的症状进行观察,收集到咳嗽、发热和呼吸急促等症状。
观察到这些症状后,医生可以使用贝叶斯定理更新对肺炎的后验概率:
如果进一步进行胸部X光检查,并获得结果,可以再一次使用贝叶斯定理更新对肺炎的诊断:
不确定性在不同变量之间逐级传递。症状的不确定性影响到疾病的诊断,而检查结果又进一步影响到对疾病的确认。
设有如下知识:
已知:
求:
利用结合不确定合成求解
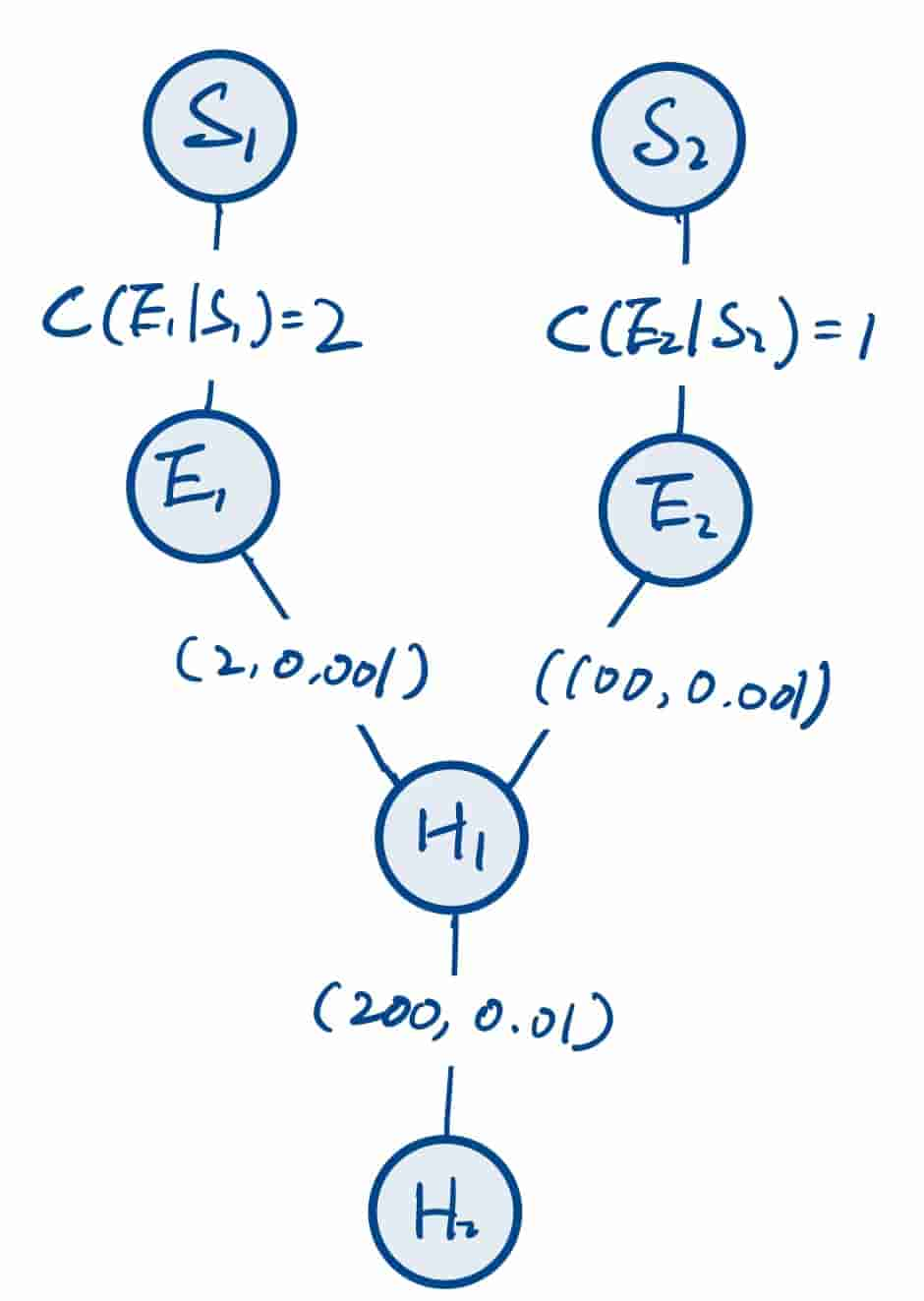
可见,证据需要观测的支持,而结论需要证据支持。
需要先用和求出,再根据求出结果。
要求出,就要先求和。
先算:
根据
得
再使用公式:
因为,
最后合成时要用这个公式:
所以要求出:
对于同理可得:
根据合成规则算:
现在算:
使用公式:
这是直接把当用了。
这个公式推导过程如下:
首先根据贝叶斯公式,
分解:
表示概率修正,反映了在给定和下额外的信息增益。
我不知道更深入的需不需要学,这一块先搁置。
根据经验对一个事物和现象为真的相信程度称为可信度。
可信度带有较大的主观性和经验性,其准确性难以把握。但人工智能面向的多是结构不良的复杂问题,难以给出精确的数学模型,先验概率及条件概率的确定又比较困难。所以可信度方法是一种比较实用的方法。
知识用产生式规则表示:
其中是该知识的可信度。称为可信度因子或规则强度,即静态强度。一般。
证据的不确定性用可信度因子表示:
表示证据的强度,即动态强度;表示知识的强度,即静态强度。
i
证据的强度通常是基于当前信息的质量和数量。当新的信息或观测数据出现时,证据的强度可以变化。例如,在医疗诊断中,随着新的症状被观察到,或新的检查结果被获得,关于病人是否患某种疾病的证据强度会发生改变。
知识被视为某种信念或真理的集合,是一种真理。通常是建立在经过验证的经验、理论或逻辑推理之上的。知识一旦被确立,就相对固定,虽然它可能在之后被更新或修正,但在某个特定时间点上,知识的强度是稳定的。
结论的可信度为:
可信度最低为0。
其中是可信度,范围。
是阈值,明确规定了知识运用的条件:只有当时,该知识才能够被应用。的取值范围为 。
证据E的可信度仍为,但其取值范围为:,因为如果在之间,则不会超出。
当时,
i
表示证据为真的条件下结论为真的可能性。
设有多条规则有相同的结论,即
如果这条规则都满足:,且都被启用,则首先分别对每条知识规则求出;然后求结论的综合可信度。
可采用如下极大值法:
或加权求和:
或有限和:
或递推:
知识前件中各个子条件地位可以不平等:
如果 学生善于思考
并且 动手能力强
并且 经常上自习
并且 坚持锻炼身体
并且 不抽烟
那么 该生是一位比较好的学生
其中是加权因子,是阈值,其值均由专家给出。所有加权因子的和应为1:
若有证据:
其可信度为:
当时,结论的可信度:
设有如下知识:
其中:
求出。
根据可信度公式
算出的可信度,并验证是否可被应用:
=都可被应用。之后根据算出:
在中,相当于,刚才又算出,所以
同理可得
代入得:
前述的几种不确定性推理方法,没有在知识中指出前提条件或者子条件的可信度值,它们都是在前提条件为真的前提下为取值。在实际中,这样有时不能准确反映领域专家的知识。
是对子条件指出的可信度,由专家给出。证据的可信度记为。
若所有则前提条件必然匹配;
若或部分小于则能否匹配取决于λ值。
简单、直观;但是专家指定可信度因子,主观片面,随推理延伸误差越来越大。