Meta Learning

這次學習並非清湯寡水，今天看理論，明天讀代碼，三位大廚正在全力烹飪。

concept

Meta-learning means "learn to learn", and while normal deep learning learns the function f, meta-learning learns how to get the function f.

	target	input	function	output	workflow
Machine learning	Find the mapping f between x and y through the training data	x	f	y	1.initialize f; 2.load data <x, y>; 3.calculate loss, optimize f; 4.find y=f(x)
Meta learning	Find a function f that generates the relation F by training the task and the data	Training tasks and their data	F	f	1.initialize F; 2.load training tasks T and their data D, optimize F; 3.find f = F*; 4.in the new task: y = f(x)

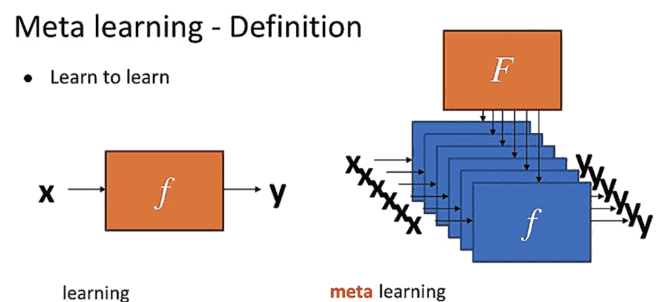
In machine learning, there is only one layer of training, which directly uses data as the training unit, but in meta-learning, the first layer of training unit is the task, and the second layer is the data (in fact, only a small amount of training is needed to the second layer, and the data obtained from the first layer can be directly processed to adapt to new tasks quickly, which is also known as fee-shot learning).

Bi-level optimization

Meta-training can be formalized as bi-level optimization:

$$\begin{array}{}\text{(outerloop)}& {\omega }^{\ast }=\underset{\omega }{argmin}\sum _{i=1}^M{L}^{meta}({\theta }^{\ast (i)}(\omega ),D_{train}^{query(i)})\end{array}$$$$\begin{array}{}\text{(innerloop)}& s.t.{\theta }^{\ast (i)}(\omega )=\underset{\theta }{argmin}{L}^{task}(\theta ,\omega ,D_{train}^{support(i)})\end{array}$$

Meta-testing for new task $j$ can be formalized as:

$${\theta }^{\ast }=\underset{\theta }{argmin}{L}^{task}(\theta ,{\omega }^{\ast },D_{test}^{support(j)})$$

Firstly, the meta-training set is divided into Support set and Query set. w can be viewed as an algorithm; θ can be considered as a model parameter.

In the Inner loop optimization stage, in the support set, the w algorithm is used to optimize θ parameters according to the performance of the loss value of the task. Finally, the optimal θ' value is obtained by the inner optimization according to the minimum $L$ task value.

In the Outer loop optimization stage, in the query set, the current Lmeta value is calculated according to the optimal θ 'value of the inner layer optimization. After multiple tasks, the minimum total loss value of all tasks is calculated to optimize the w parameter, and the $w$ algorithm is constantly adjusted to achieve the optimal performance in all tasks.

The inner layer optimization deals with ordinary machine learning problems, and the outer layer takes the results of the inner layer as data to obtain the parameters of the metamodel, that is, the "hyperparameters" of ordinary machine learning problems.

Intensive reading of thesis

Source: https://arxiv.org/abs/1703.03400

MAML

Problem Set-Up

The goal of few-shot meta-learning is to train a model that can quickly adapt to a new task using only a few datapoints and training iterations.

consider a model, denoted $f$ , that maps observations $x$ to outputs $a$.

A generic notion of a learning task:

Each task

$$\mathcal{T}=\{\mathcal{L}(x_1,a_1,...,x_H,a_H),q(x_1),q(x_{t+1}|x_t,a_t),H\}$$

consists of a loss function $\mathcal{L}$, a distribution over initial observations $q(x1)$, a transition distribution $q(x_{t+1}|x_t,a_t)$, and an episode length $H$.

In supervised learning problems, the length $H=1$. The loss $\mathcal{L}(x_1,a_1,...,x_H,a_H)\to \mathbb{R}$​​, provides task-specific feedback, which might be in the form of a misclassification loss or a cost function in a Markov decision process.

During meta-training, a task ${\mathcal{T}}_i$ is sampled from $p(\mathcal{T})$, the model is trained with $K$ samples and feedback from the corresponding loss ${{\mathcal{L}}_{\mathcal{T}}}_i$ from ${\mathcal{T}}_i$ and then tested on new samples from ${\mathcal{T}}_i$. The test error on sampled tasks ${\mathcal{T}}_i$ serves as the training error of the meta-learning process. That is, the "errors" of the inner training are also used as meta-training data, so that the meta-learning model knows: if the parameters of the task are designed in this way, what will be the consequences? Gradually the meta-learning model can be designed better and better. After the K round of training, new tasks are used to evaluate the results.

MAML

The intuitive analysis of this algorithm is that there must be an internal pattern that is most transferrable, just find it.

Meta-learning is also based on gradient descent, so it is only necessary to find the parameters that are sensitive to task changes, and when they change, the task loss under the task set will be greatly affected.

When faced with a particular task, parameter $\theta$ will choose different values according to the gradient, and when adapted to task ${\mathcal{T}}_i$, $\theta$ will become ${\theta }_i^{\ast }$, which is the ideal effect.

Consider a model represented by a parametrized function $f_{\theta }$ with parameters $\theta$. When adapted to task ${\mathcal{T}}_i$, $\theta$ will become ${\theta }_i^{\prime }$​.

We will update ${\theta }_i^{\prime }$ according to the classical gradient descent method:

$${\theta }_i^{\prime }=\theta -\alpha {\mathrm{\nabla }}_{\theta }{{\mathcal{L}}_{\mathcal{T}}}_i(f_{\theta })$$

${{\mathcal{L}}_{\mathcal{T}}}_i(f_{\theta })$ is the loss of the model on ${\mathcal{T}}_i$, and ${\mathrm{\nabla }}_{\theta }{{\mathcal{L}}_{\mathcal{T}}}_i(f_{\theta })$ is the gradient of $\theta$ on this loss function.

Our task(meta-objective) now becomes to find a specific $\theta$ that minimizes the sum of $f_{{\theta }_i^{\prime }}$'s losses on all tasks:

$$\underset{\theta }{min}\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{{\mathcal{L}}_{\mathcal{T}}}_i(f_{{\theta }_i^{\prime }})=\sum _{{\mathcal{T}}_i}(f_{\theta -\alpha {\mathrm{\nabla }}_{\theta }{{\mathcal{L}}_{\mathcal{T}}}_i(f_{\theta })})$$

Meta optimization is the optimization of $\theta$, using the updated ${\theta }^{\prime }$ to calculate meta-objective. We want to have some optimal parameters determined at the end of each round of training.

The meta-optimization across tasks is performed via SGD, the model parameters $\theta$ are updated as follows:

$$\theta \leftarrow \theta -\beta {\mathrm{\nabla }}_{\theta }\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{{\mathcal{L}}_{\mathcal{T}}}_i(f_{{\theta }_i^{\prime }})$$

where $\beta$​​​ is the meta step size.

Pseudocode of MAML

randomly initialize $\theta$ while not done do  sample batch of tasks ${\mathcal{T}}_i\sim p(\mathcal{T})$  for all ${\mathcal{T}}_i$ do   evaluate ${\mathrm{\nabla }}_{\theta }{{\mathcal{L}}_{\mathcal{T}}}_i(f_{\theta })$ with respect to $K$ examples   compute adapted parameters with gradient descent: ${\theta }_i^{\prime }=\theta -{\mathrm{\nabla }}_{\theta }{{\mathcal{L}}_{\mathcal{T}}}_i(f_{\theta })$  end for  update $\theta \leftarrow \theta -\beta {\mathrm{\nabla }}_{\theta }\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{{\mathcal{L}}_{\mathcal{T}}}_i(f_{{\theta }_i^{\prime }})$ end while

Since the update of the metagradient goes through two loops (updating the outer gradient by the gradient of the inner layer), an additional reverse pass through $f$​ is required to compute the Hessian-vector product.

About Hessian-vector product

A Hessian matrix is a matrix consisting of the second partial derivatives of a function whose independent variables are vectors.

Consider a function:

$$f(x_1,x_2,...,x_n)$$

If all the second partial derivatives of $f$ exist, then the $i{j}^{th}$ term of the Hessian matrix of $f$ is:

$$H(f{)}_{ij}(x)=D_i{D}_{j}f(x)$$

where $x=(x_1,x_2,...,x_n)$,

$$H(f)={\left[\begin{array}{cccc}\frac{{\partial }^{2}f}{\partial x_1^2}& \frac{{\partial }^{2}f}{\partial x_1\partial x_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_1\partial x_n}\\ \frac{{\partial }^{2}f}{\partial x_2\partial x_1}& \frac{{\partial }^{2}f}{\partial x_2^2}& \cdots & \frac{{\partial }^{2}f}{\partial x_2\partial x_n}\\ ⋮& ⋮& \ddots & ⋮\\ \frac{{\partial }^{2}f}{\partial x_n\partial x_1}& \frac{{\partial }^{2}f}{\partial x_n\partial x_2}& \cdots & \frac{{\partial }^{2}f}{\partial x_n^2}\end{array}\right]}_{nn}$$

For a set of parameters $x_1,x_2,...,x_n$, then the model is $f(x_1,x_2,...,x_n)$​.

In meta-learning, the outer layer optimization involves the results of the inner layer optimization, which leads to the gradient of the outer layer loss function not only dependent on the current model parameters, but also on how the model is optimized by updating the inner layer gradient. Therefore, the gradient calculation of the outer layer optimization usually contains second-order derivative information, so the Hessian matrix is required. However, computing the complete Hessian matrix faces a huge complexity of $O(n^2)$, so to use the Hessian vector product, it is possible to approximate these second-order gradients in a single backpropagation without actually constructing and inverting the complete Hessian matrix. Here I omit how does the Hessian vector product compute the second order gradient around the Hessian matrix.

Species of MAML(apply)

Supervised Regression and Classification

Few-shot learning makes it possible to use only a small amount of data to perform classification tasks, such as recognizing cats based on a large number of other types of objects that it have seen before.

Since the model accepts a single input and produces a single output, rather than a sequence of inputs and outputs, we can define the horizon $H=1$ (episode length) and drop the timestep subscript on $x_t$. The task generates $K$ observations $x$ from $q_i$, and the loss is represented by the error between the model's output for $x$ and corresponding target values $y$​ for that observation and task.

Two common loss functions used for supervised classification and regression are cross-entropy and mean-squared error(MSE):

$$\begin{array}{}\text{(MSE loss)}& {{\mathcal{L}}_{\mathcal{T}}}_i(f_{\varphi })=\sum _{x^{(j)},y^{(j)}\sim {\mathcal{T}}_i}||f_{\varphi }(x^{(j)}-y^{(j)})|{|}_2^2\end{array}$$

where $x^{(j)}$, $y^{(j)}$ are an i/o pair sampled from task ${\mathcal{T}}_i$. In $K$-shot regression tasks, $K$​ i/o pairs are provided for learning for each task.

For discrete classification tasks with a cross entropy loss:

$$\begin{array}{}\text{(cross-entropy loss)}& {{\mathcal{L}}_{\mathcal{T}}}_i(f_{\varphi })=\sum _{x^{(j)},y^{(j)}\sim {\mathcal{T}}_i}{y}^{(i)}log{f}_{\varphi }(x^{(j)})+(1-y^{(j)})log(1-f_{\varphi }(x^{(j)}))\end{array}$$

K-shot classification tasks use $K$ input/output pairs from each class, for a total of $NK$ datapoints for $N$​-way classification.

Pseudocode of MAML for Few-Shot Supervised Learning

randomly initialize $\theta$ while not done do  sample batch of tasks ${\mathcal{T}}_i\sim p(\mathcal{T})$  for all ${\mathcal{T}}_i$ do   Sample $K$ datapoints $\mathcal{D}=\{x^{(j)},y^{(j)}\}$ from $ \mathcal{T}_i$   Evaluate ${\mathrm{\nabla }}_{\theta }{{\mathcal{L}}_{\mathcal{T}}}_i(f_{\theta })$ using $\mathcal{D}$ and ${{\mathcal{L}}_{\mathcal{T}}}_i$   Compute adapted parameters with gradient descent: ${\theta }_i^{\prime }=\theta -\alpha {\mathrm{\nabla }}_{\theta }{{\mathcal{L}}_{\mathcal{T}}}_i(f_{\theta })$   Sample datapoints ${\mathcal{D}}_i^{\prime }=\{x^{(j)},y^{(j)}\}$ from $ \mathcal{T}_i$ for the meta-update  end for  Update $\theta \leftarrow \theta -\beta {\mathrm{\nabla }}_{\theta }\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{{\mathcal{L}}_{\mathcal{T}}}_i(f_{{\theta }_i^{\prime }})$ using each $ \mathcal{D}_i'$ and ${{\mathcal{L}}_{\mathcal{T}}}_i$ end while

Reinforcement Learning(MDP)

Reinforcement learning is a learning mechanism that learns how to map from state to behavior in order to maximize the reward obtained. Such an agent needs to continuously experiment in the environment and optimize the state-behavior correspondence through the feedback (reward) given by the environment.

Each RL task ${\mathcal{T}}_i$ contains an initial state distribution $q_i(x_1)$ and a transition distribution $q_i(x_{t+1}|x_t,a_t)$, and the loss $ \mathcal{L_T}_i$ corresponds to the reward function $R$. The entire task is a Markov decision process(MDP) with horizon $H$. The model being learned, $f_{\theta }$, is a policy that each maps from states $x_t$(The current environment) to a distribution over actions $a_t$(Actions that can be taken in the current state, here are adjustments to the parameters) at each timestep $t\in \{1,2,...,H\}$. The loss for task $ \mathcal{T}_i$ and model $f_{\varphi }$ takes the form

$${{\mathcal{L}}_{\mathcal{T}}}_i(f_{\varphi })=-{\mathbb{E}}_{x_t,a_t\sim f_{\varphi },q_{{\mathcal{T}}_i}}[\sum _{t=1}^H{R}_i(x_t,a_t)]$$

Notice that instead of using the loss function directly, we've created an artificial loss function by first calculating the reward and then taking the negative sign.

$K$ rollouts from $f_{\theta }$ and task $ \mathcal{T}_i$, $(x_1,a_1,...,x_H)$, and the corresponding rewards $R(x_t,a_t)$, may be used for adaptation on a new task $ \mathcal{T}_i$.

The reward function is usually not differentiable, and the loss function is not differentiable. We use policy gradient method s to estimate the gradient both for the model gradient update(s) and the meta-optimization. In the strategy gradient algorithm, the input to the strategy function is the state ss and the action a aa, and the output is a probability value between 0 and 1. A later article will explain how the strategy gradient is implemented.

Pseudocode of MAML for Reinforcement Learning

randomly initialize $\theta$ while not done do  sample batch of tasks ${\mathcal{T}}_i\sim p(\mathcal{T})$  for all ${\mathcal{T}}_i$ do   Sample $K$ trajectories $\mathcal{D}=\{(x_1,a_1,...x_H)\}$ using $f_{\theta }$ in $ \mathcal{T}_i$   Evaluate ${\mathrm{\nabla }}_{\theta }{{\mathcal{L}}_{\mathcal{T}}}_i(f_{\theta })$ using $\mathcal{D}$ and ${{\mathcal{L}}_{\mathcal{T}}}_i$   Compute adapted parameters with gradient descent: ${\theta }_i^{\prime }=\theta -\alpha {\mathrm{\nabla }}_{\theta }{{\mathcal{L}}_{\mathcal{T}}}_i(f_{\theta })$   Sample trajectories ${\mathcal{D}}_i^{\prime }=\{(x_1,a_1,...x_H)\}$ using $f_{{\theta }_i^{\prime }}$ in $ \mathcal{T}_i$  end for  Update $\theta \leftarrow \theta -\beta {\mathrm{\nabla }}_{\theta }\sum _{{\mathcal{T}}_i\sim p(\mathcal{T})}{{\mathcal{L}}_{\mathcal{T}}}_i(f_{{\theta }_i^{\prime }})$ using each $ \mathcal{D}_i'$ and ${{\mathcal{L}}_{\mathcal{T}}}_i$ end while

This algorithm has the same structure as Algorithm 2, with the principal difference being that steps 5 and 8 require sampling trajectories from the environment corresponding to task $ \mathcal{T}_i$.

Experimental Evaluation

I will not explain this part in detail, but a set of graphs is given in the original paper, which can be seen that the model using MAML has understood the characteristics of sine waves: