A*算法

算法目的

找到从起点到终点间的最短（最优）路径。

流程

初始化搜索区域

把搜索区域简化为二维数组，数组每一个元素的状态都只有可走和不可走。每一个元素被称为节点，也就是实际图中每一个块的中心点。

搜索

① 从起点A开始，把起点节点加入open list（关注集）。open list是待检查的列表，后期只会从这个列表中找节点作为起始向外扩张。

② 检查所有与A相邻的方格，把其中所有可走的格都加入open list，并把A设为这些方格的父节点。

③ 把A从open list移除，加入close list。close list中的格子都不再需要关注。

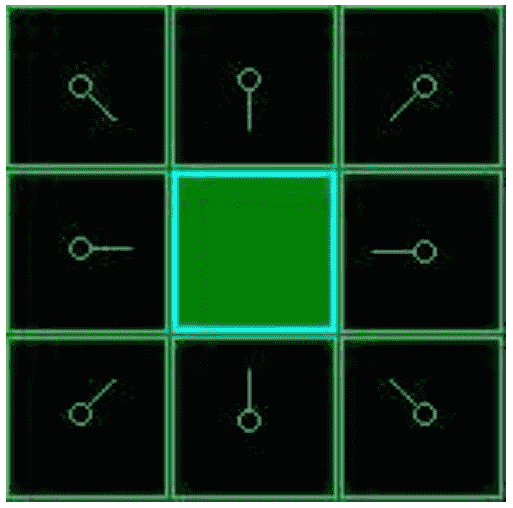
如图，与A相邻的格子都加入了open list，并记录自己的父节点A（图中用可视化指针表示），同时A已经被移出open list，后续不用再关注。

④ 之后需要从open list中找一个格子作为起点。重复之前的步骤。但是区别于dijkstra算法，并不需要遍历全部的open list，而是有目的、有优先级地去访问。那么这个优先级根据什么来定呢，是根据$F$的值来定。

路径排序

$F$值的计算

$$F=G+H$$

其中$G$表示从起点到当前节点的代价。

如果是上下左右相邻的格子（曼哈顿距离为 1），那么移动成本为 10。如果是对角线相邻的格子（曼哈顿距离为 $\sqrt{2}$），那么移动成本为10 的 $\sqrt{2}$ 倍（通常近似为14）。

$H$​值是当前节点到目标节点的预估代价（横竖走过去的最短路）。

如图中①、②格子所示，$H$值只需要简单地算曼哈顿距离即可，不用考虑墙。

继续搜索

⑤ 从上述步骤中找出$F$值（总代价）最小的格子，放入close list（因为马上要开始分析它周围的所有格子，它本身作为起点不再有分析价值）。

⑥ 检查所有与它相邻的方格，忽略其中在 close list 中或是不可走的方格，如果方格不在open list 中，则把它们加入到 open list 中。

注意

一个节点一旦被加入了open list，那它的$G$和$H$值以及父节点都永远不会再改变，除非有更短的路径经过这个节点。

由于此时它周围的所有格子都已经在open list中，所以不做改变，也无需更新$G$值：

$G$值更新

$G$值是到起点的距离值。新加入open list的格子的$G$值应该是它到父节点的$G$值加上父节点本身的$G$值。

下一步，找$F$值最小的格子重复上述部分，其实右上和右下都可以选，这里选右下：

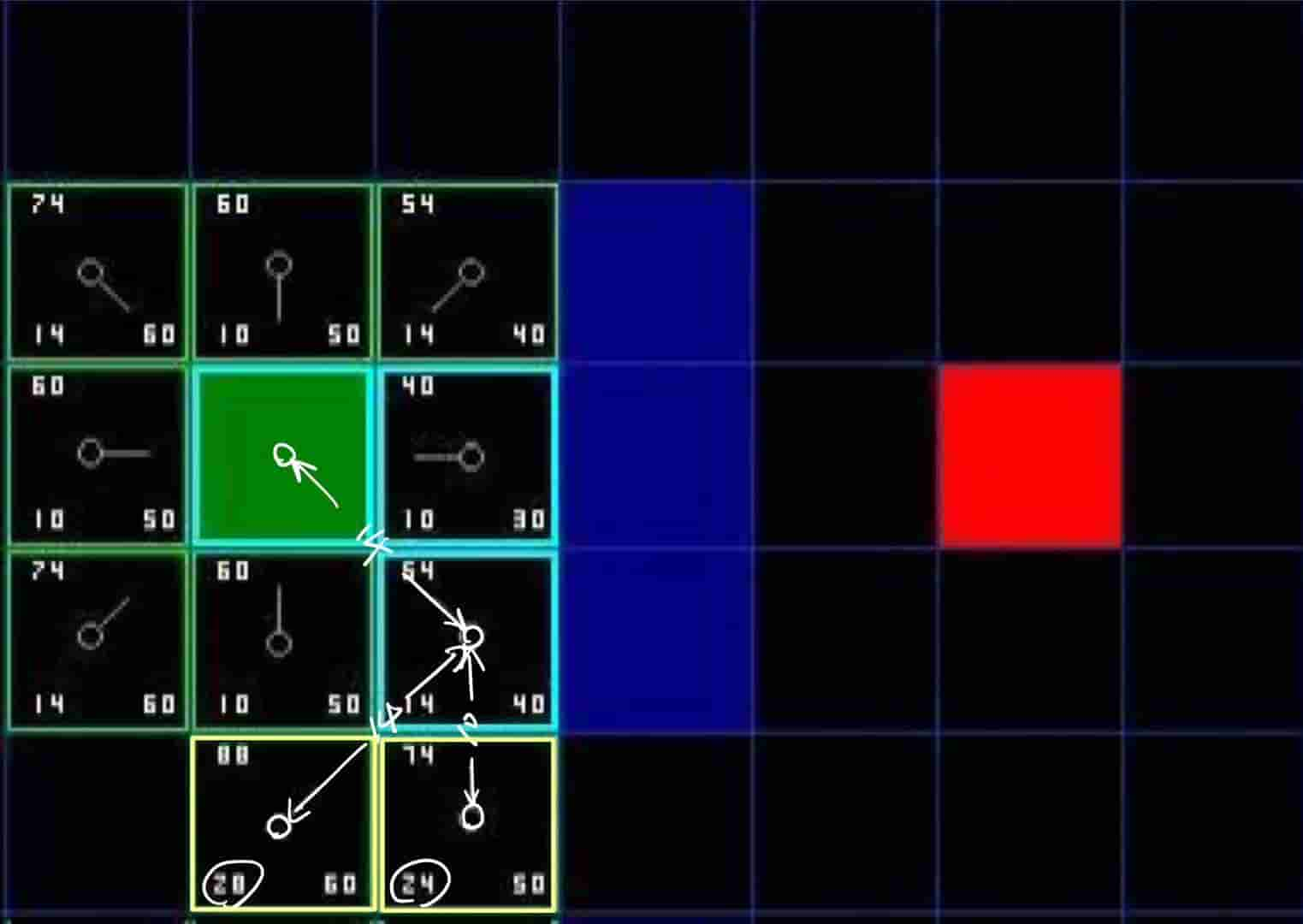
检查它周围的格子发现有两个不在open list，于是把它们加入。左边的格子到它父节点的距离是14，它的父节点$G$值是14，所以它的$G$值是28。

i

墙正下方的格子在这里被认为是不可达的。因为这么走和墙角的距离为0，会碰到墙角。

但是在其他的情况下又有可能可达，比如一些奇形怪状的节点可以确保穿越墙角时不碰到。

之后按这个方法不断搜索，直到找出最短路：

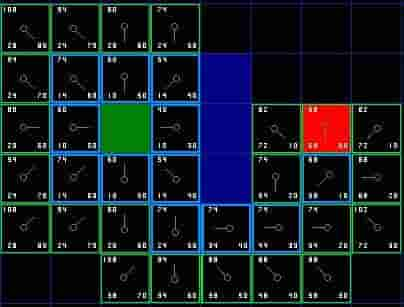
这里蓝色格子是close list。现在只是搜到了终点。为了得到路径，只需从终点开始按父节点指针回溯到起点：

例子

可见，如果一个节点在新的父节点的open list中可以拥有更小的$f$值，那它就会认新父亲：

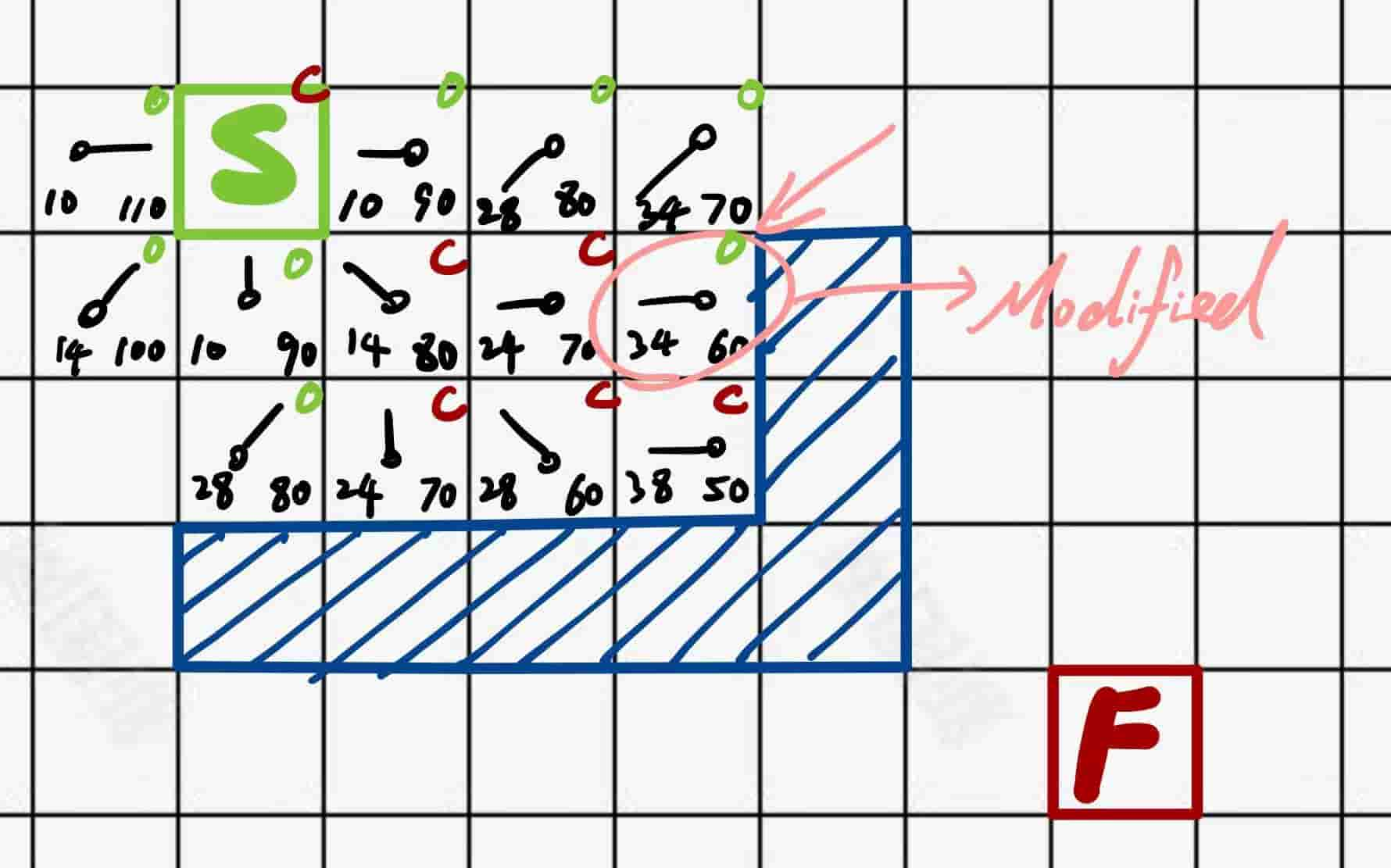
启发函数

概念

上边说根据公式

$$F=G+H$$

确定优先级，但是可以把每个变量都扩展成函数：

$$f(n)=g(n)+h(n)$$

$h(n)$是节点$n$距离终点的预计代价，也就是启发函数。

对算法的影响

各种情况

① 当启发函数$h(n)=0$时，

$$f(n)=g(n)$$

也就是在搜索过程中不考虑与目标的距离，而是以起点为中心公平地向四周搜索，此时退化为了Dijkstra算法。Dijkstra 算法总是找到最短路径，但它没有启发性估计，所以通常会遍历更多节点，效率较低。

② 当$h(n)=\mathrm{实}\mathrm{际}\mathrm{代}\mathrm{价}$，也就是上面说的按曼哈顿距离作为$h(n)$的值。此时 A* 算法不仅可以找到最优路径，而且速度最快。这是因为此时启发函数的估计完全准确，算法不需要多余的节点扩展，直接沿着最佳路径进行搜索。

然而，在实际情况中，往往难以精确估计到目标节点的实际代价，尤其在没有到达目标节点之前，这种理想情况较难实现。

③ 当$h(n)\le \mathrm{实}\mathrm{际}\mathrm{代}\mathrm{价}$，它不会高估到目标节点的成本。算法能保证找到最优解，但是会搜索更多的格子导致速度变慢。

为什么这种情况能保证最优解？

既然$f(n)=g(n)+h(n)$，那么$f(n)$就只依赖于$g(n)$和$h(n)$。$h(n)$更小，$f(n)$就更依赖于$g(n)$，这时候它会更少地考虑到目标的距离，而只看自己与起点的距离。如果从起点往外找，那一定能用最小的代价扩散到目标。设想极限情况，当$h(n)$​​足够小，小到无限接近0，那此时就变成dijkstra算法，这样是绝对能找到最短路的。

④ 当$h(n)>\mathrm{实}\mathrm{际}\mathrm{代}\mathrm{价}$，算法不能保证找到最优解，但是会更快。

为什么这种情况能不保证最优解？

相反，当$h(n)$偏大，$f(n)$就更依赖$h(n)$，会更多地考虑自己到目标的距离怎么才能更短。但是注意，上边说过在计算$h(n)$​时，一般是不考虑障碍物而直接去算曼哈顿距离或直线距离的。这样一来就会让算法眼里只有目标，会盲目朝着目标走，直到撞墙。

⑤ 当$h(n)\gg g(n)$，$f(n)$会全部依赖于启发函数$h(n)$，这样算法就退化成最佳优先搜索（BFS）。因为此时搜索完全被目标吸引，完全忽略障碍的存在。

图解

情况①，当启发函数$h(n)=0$：

算法只关心当前格子和起点的距离，搜索时会经常出现两个格子距离一样的情况，而算法又必须优先搜索最小的，所以就要经常左右横跳去搜，很慢。

情况②，当启发函数等于实际代价：

这种情况下会多走一些弯路，但是最终也能找到最短路。

情况③，当启发函数占主导：

这张图错了，右边那里还是会走斜线！

这时候如果只按启发函数值来搜，就可能发生图中的情况，它可能搜索的格子更少，但是会被启发函数误导，找到的并不是最短路。

伪代码

伪代码

A* Algorithm
起点放入open list while true  if open list为空:   搜索失败，结束  取open list中$f(n)$最小的节点加入close list  if 节点为终点:   返回路径，结束  遍历当前不在close list中的节点  if 节点在open list里:   更新$g(n)$值  else   计算当前节点$g(n)$、$h(n)$值并加入open list

python实现

Question

不知道是否需要。

复杂度

A*算法的时间和空间复杂度都为：

$$O(b^d)$$

其中$b$是节点分支系数，即每个节点有多少邻居节点；$d$是从起点到目标的深度（就是路径长度）。

因为每搜一步，就要遍历当前所有open list的节点，越往后这个数字会指数级增加。

如果启发函数$h(n)$是完美的，即它等于实际代价，则复杂度能接近$O(d)$。因为此时它不再需要遍历其它无关的节点；

如果$h(n)=0$，算法退化为Dijkstra算法，复杂度就是$O(b^d)$，因为它需要遍历所有相邻节点。

可视化

BUG!!!

我正在研究怎么把html模板嵌入进来，这部分功能暂不提供。

A*算法的性质

定理一

当问题有解时，A*算法一定能找到最佳路径。对有限图，如果从初始节点$s$到目标节点$t$​有路径存在，则A*算法一定成功结束。

引理一

对无限图，若有从初始节点s到目标节点t的路径，则A*不结束时，在OPEN表中即使最小的一个f值也将增到任意大，或有$f(n)>f^{\ast }(s)$​。

算法不结束，也就是会搜到更多的点，图中的节点可能是无限的，那么$f$值多大都有可能。而$f^{\ast }(s)$是初始节点到目标节点的预估代价，$f(n)>f^{\ast }(s)$代表有些点的代价被高估了（因为正常情况下中间点到目标的最优路径不可能比从初始点走还长，也就是没找到最优路径）。

引理二

A*结束前，OPEN表中必存在$f(n)\le f^{\ast }(s)$的结点（$n$是在最佳路径上的结点），也就是必存在一个在最优路径上的节点：

对于一个在最优路径上的节点$n$：$f(n)=g(n)+h(n)$，$g(n)$是实际代价，$h(n)$​是启发估计；

若$g^{\ast }(n)$是最优估计，对于在最优路径上的点自然$g^{\ast }(n)=g(n)$，

$f(n)=g^{\ast }(n)+h(n)\le g^{\ast }(n)+h^{\ast }(n)=f^{\ast }(n)=f^{\ast }(s)$，即$f(n)\le f^{\ast }(s)$。

疑点

$f(n)=g^{\ast }(n)+h(n)\le g^{\ast }(n)+h^{\ast }(n)$ 这个结论怎来的？$n$又不一定是出发点，为什么$f^{\ast }(n)=f^{\ast }(s)$？

定理二

对无限图，若从初始节点s到目标节点t有路径存在，则A*一定成功结束。

利用引理一、二证矛盾：

根据引理一，若A*不结束，则open中所有的点都有：$f(n)>f^{\ast }(s)$；

根据引理二，A*结束前必存在节点n使得$f(n)\le f^{\ast }(s)$​，所以如果A*不能结束，就会导致矛盾。

推论一

open表上任何具有$f(n)<f^{\ast }(s)$的节点n最终都会被A*选做需要扩展的节点。

i

证明暂略。

定理三，可采纳性定理

若存在从初始节点s到目标节点t有路径，则A*必能找到最佳解结束。

推论二

对于被A*选作扩展的任一节点n，有$f(n)\le f^{\ast }(s)$。

定理四

设对同一个问题定义了两个A*算法$A_1$和$A_2$，若$A_2$比$A_1$有较多的启发信息，即对所有非目标节点有$h_2(n)>h_1(n)$，则：

在具有一条从s到t的路径的隐含图上，搜索结束时，由$A_2$所扩展的每一个节点，也必定由A1所扩展，即$A_1$扩展的节点数至少和$A_2$一样多。

启发信息更少，就说明算法倾向于求稳，它会在扩展一些节点的基础上额外扩展一些来保证最优解。

如果$h_2(n)>h_1(n)$ (目标节点除外)，则$A_1$扩展的节点数$\ge A_2$扩展的节点数

A*算法改进

存在问题

对于已在open中的点，如果发现它在有新父亲的情况下需要更新父亲节点并重新放入open，这会导致某些节点被反复修改指针和$f$值，使效率下降。这种现象称为出现多次扩展节点。

原因是在前面的扩展中，并没有找到从初始节点到当前节点的最短路径。

解决

改进的条件

可采纳性不变；不多扩展节点；不增加算法的复杂性。

限制h

对h增加适当的限制，使得第一次扩展一个节点时，就找到了从s到该节点的最短路径。

对一个启发函数h，如果对所有节点$n_i,n_j$，其中$n_j$是$n_i$的子节点，有：

$$\{\begin{array}{c}h(n_i)-h(n_j)\le c(n_i,n_j)\\ h(t)=0\end{array}$$

则称h单调。

定理五

若$h(n)$是单调的，则A*扩展了节点n之后，就已经找到了到达节点$n$的最佳路径。

即：当A*选$n$扩展时，有$g(n)=g^{\ast }(n)$​。

定理六

若$h(n)$是单调的，则由A*所扩展的节点序列其f值是非递减的。即$f(n_i)\le f(n_j)$。

疑问

这个单调性是什么意思？直观体现？单调性有关的定理是为什么？

改进算法

根据推论一和推论二：

OPEN表上任一具有$f(n)<f^{\ast }(s)$的节点定会被扩展；A*选作扩展的任一节点，定有$f(n)\le f^{\ast }(s)$​。

这样可以把open表中的所有点分为两类：

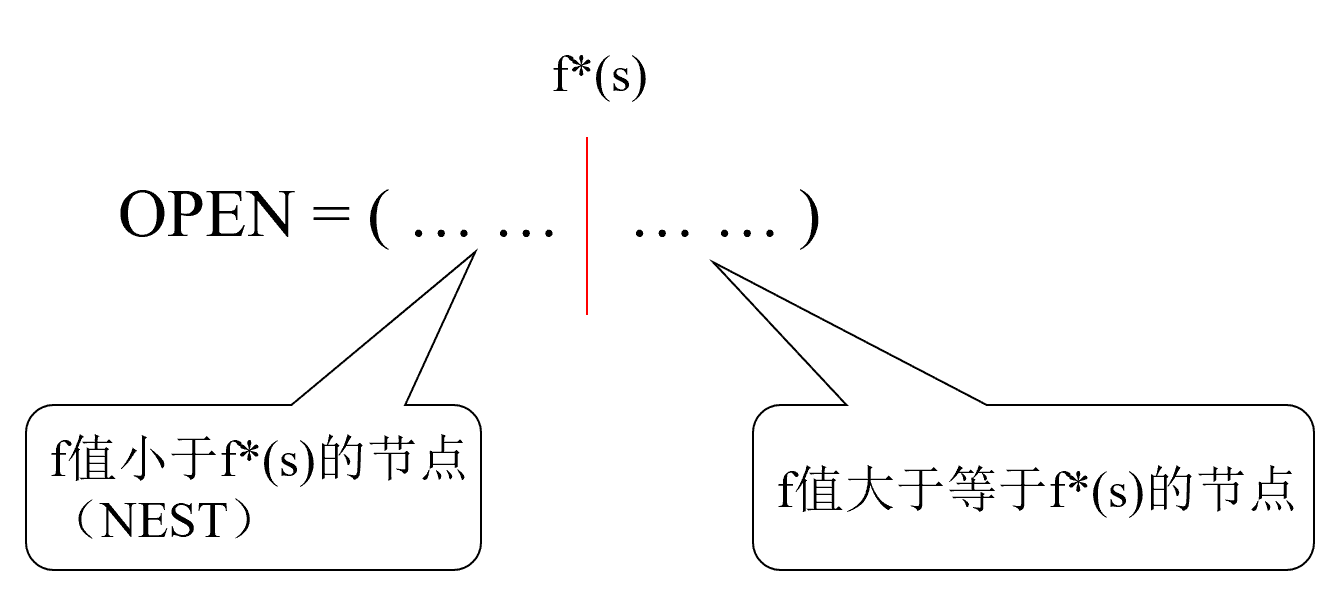
设$f_m$是到目前为止已扩展节点的最大$f$值，用$f_m$代替$f^{\ast }(s)$。

修正后的评估过程
open=$(s)$, $f(s)=g(s)+h(s)$, $f_m=0$; loop  if open is empty then exit with fail;  nest = $\{n_i|f(n_i)<f_m\}$  if nest is not empty then n = nest中$g$值最小的节点;  else n = first(open), $f_m=f_n$;

其实就是在从open中拿节点时优先拿$g$值小于$f_m$的。