确定性推理
确定性推理
基本概念
推理方式
从推出结论的途径划分:演绎、归纳、默认
演绎
从全称判断推导出单称判断的过程,由一般知识推理细化出适合某一情况的结论。从一般到个别。
三段论式
大前提:足球运动员都很强壮
小前提:高波是一名足球运动员
结论:高波身体强壮
归纳
从足够多的事例中归纳出一般性结论的推理过程。从个别到一般。
完全归纳:考虑全部对象后得出结论。是必然性推理。
不完全归纳:抽检,未考虑全部对象。是非必然性推理。
默认(缺省推理)
在知识不完全时假设某些条件已具备。
例如设计鸟笼,不确定要关的鸟会不会飞,先默认会飞,推出鸟笼要加盖子的结论。
按推理时所用知识的确定性划分:确定性、不确定性推理
确定性推理
所用的知识和证据都确定,结论也确定。真值只有真假两种。
不确定推理
所用的知识和证据都不确定,结论也不确定。真值不只有真假两种。
现实世界中的事物和现象大都是不确定的,或者模糊的,很难用精确的数学模型来表示与处理。不确定性推理又分为似然推理与近似推理或模糊推理,前者是基于概率论的推理,后者是基于模糊逻辑的推理。人们经常在知识不完全、不精确的情况下进行推理,因此,要使计算机能模拟人类的思维活动,就必须使它具有不确定性推理的能力。
按推理过程中推出的结论是否越来越接近最终目标划分:单调、非单调推理
单调推理
单调推理是在推理过程中随着推理向前推进及新知识的加入,推出的结论越来越接近最终目标。单调推理的推理过程中不会出现反复的情况,即不会由于新知识的加入否定了前面推出的结论,从而使推理又退回到前面的某一步。
非单调推理
非单调推理是在推理过程中由于新知识的加入,不仅没有加强已推出的结论,反而要否定使推理退回到前面的某一步,然后重新开始。
非单调推理一般是在知识不完全的情况下发生的。由于知识不完全,为使推理进行下去,就要先作某些假设,并在假设的基础上进行推理。当以后由于新知识的加入发现原先的假设不正确时,就需要推翻该假设以及由此假设推出的所有结论,再用新知识重新进行推理。显然,默认推理是一种非单调推理。
在人们的日常生活及社会实践中,很多情况下进行的推理都是非单调推理。明斯基举了一个非单调推理的例子:当知道X是一只鸟时,一般认为X会飞,但之后又知道X是企鹅,而企鹅是不会飞的,则取消先前加入的X能飞的结论,而加入X是不会飞的结论。
按推理中是否运用与推理有关的启发性知识划分:启发式、非启发式推理
如果推理过程中运用与推理有关的启发性知识,则称为启发式推理,否则称为非启发式推理。
所谓启发性知识是指与问题有关且能加快推理过程、求得问题最优解的知识。例如,推理的目标是要在脑膜炎、肺
炎、流感这三种疾病中选择一个,又设有r1、r2、r3这三条产生式规则可供使用,其中r1推出的是脑膜炎,r2推出
的是肺炎,r3推出的是流感。如果希望尽早地排除脑膜炎这一危险疾病,应该先选用r1;如果本地区目前正在盛行
流感,则应考虑首先选择r3。这里,“脑膜炎危险”及“目前正在盛行流感”是与问题求解有关的启发性信息。
推理方向
正向推理
正向推理是以已知事实作为出发点的一种推理。
正向推理的基本思想:从用户提供的初始已知事实出发,在知识库KB中找出当前可适用的知识,构成可适用知识集KS,然后按某种冲突消解策略从KS中选出一条知识进行推理,并将推出的新事实加入到数据库中作为下一步推理的已知事实,此后再在知识库中选取可适用知识进行推理,如此重复这一过程,直到求得了问题的解或者知识库中再无可适用的知识为止。正向推理的推理过程可用如下算法描述:
①将用户提供的初始已知事实送入数据库DB。
②检查数据库DB是否已经包含了问题的解,若有,则求解结束,并成功退出;否则,执行下一步
③根据数据库DB中的已知事实,扫描知识库KB,检查KB中是否有可适用(即可与DB中已知事实匹配)的知识,若有,则转向④,否则转向⑥。
④把KB中所有的适用知识都选出来,构成可适用知识集KS。
⑤若KS不空,则按某种冲突消解策略从中选出一条知识进行推理,并将推出的新事实加入DB 中,然后转向②;若KS空,则转向⑥。
⑥询问用户是否可进一步补充新的事实,若可补充,则将补充的新事实加入DB中,然后转向③;否则表示求不出解,失败退出。

逆向推理
逆向推理是以某个假设目标作为出发点的一种推理。
逆向推理的基本思想是:首先选定一个假设目标,然后寻找支持该假设的证据,若所需的证据都能找到,则说明原假设是成立的;若无论如何都找不到所需要的证据,则说明原假设是不成立的,为此需要另作新的假设。
逆向推理过程可用如下算法描述:
①提出要求证的目标(假设)。
②检查该目标是否已在数据库中,若在,则该目标成立,退出推理或者对下一个假设目标进行验证;否则,转下一步。
③判断该目标是否是证据,即它是否为应由用户证实的原始事实,若是,则询问用户;否贝转下一步。
④在知识库中找出所有能导出该目标的知识,形成适用的知识集KS,然后转下一步。
⑤从KS中选出一条知识,并将该知识的运用条件作为新的假设目标,然后转向②。
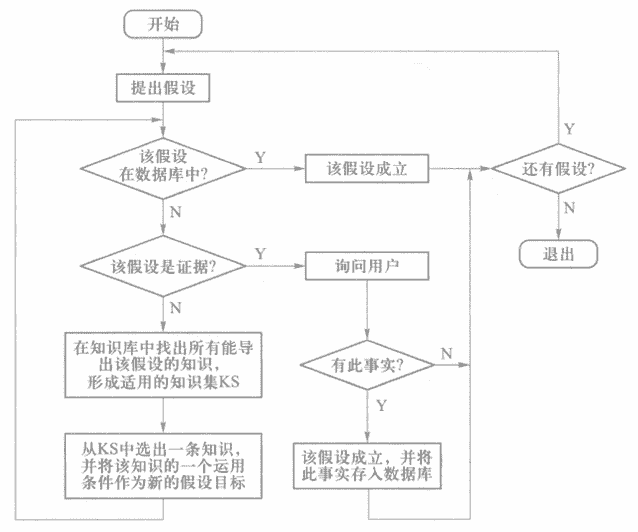
不必使用与目标无关的知识,目的性强。但起始目标只能盲目选择,如果不符合实际就要多次假设影响效率。
混合推理
以下情况需要用:
已知事实不充分、正向推出的结论可信度不高、希望得到更多结论。
先正后逆和先逆后正:

双向推理
一方面根据已知事实正向推理但不推到最终目标;另一方面从某假设出发逆向推理,但也不推至原事实,他俩在中途相遇得到中间结论。
冲突消解策略
推理过程中系统需要不断拿已知知识和知识库的知识做匹配。
三种情况
①已知事实只可以匹配知识库中的一个知识;
②已知事实不能匹配任何知识;
③已知事实可以匹配知识库中多个知识、或多个事实匹配一个知识、或多个事实匹配多个知识。
对于①,直接把这个知识用于推理。
对于②,推理无法继续。
对于③,称为发生冲突。需要按一定策略从多个知识中挑一个用于推理。
四种冲突消解策略
按规则的针对性排序
前件中条件详细(多)的规则先推。
按已知事实的新鲜性排序
新鲜事实(刚得到的局部结论)越多(越新鲜)的规则先推。
按匹配度排序
在不确定性匹配中,计算两个知识模式的相似度(匹配度),并对其排序,相似度高的规则先推。
按条件个数排序
条件少的规则先推。
自然演绎推理
从一组已知为真的事实出发,直接运用经典逻辑的推理规则推出结论的过程,称为自然演绎推理。
假言推理
拒取式推理
归结演绎原理
定理证明即证明
子句
在谓词逻辑中,把原子谓词公式及其否定统称为文字。任何文字的析取式称为子句。
子句:
不包含任何文字的子句称为空子句,永假。
任何谓词公式都可通过等价关系及推理规则化成相应的子句集。
谓词公式化为子句集
例:
1、消去蕴涵(
2、利用等价关系把
3、利用换名规则换名
4、消去存在量词
若存在量词不出现在全称量词的辖域内,则只要用一个新的个体常量替换受该量词约束的变元。
若在全称量词辖域:利用Skolem函数替换:即用一个以全程量词变元为自变量的函数换掉存在量词变元:
在这里,后边都在
5、化前束范式
把所有全称量词移到公式的左边,并使每个全称量词的辖域包括这个量词后面公式的整个部分。其实上边的已经是前束范式了:
6、化合取范式(用合取符号连接一堆析取式)
等价关系:
7、消去全称量词
到了这一步,所有余下的量词均被全称量词量化了。同时全称量词的次序也不重要了。因此,我们可以消去全称量词:
8、获取子句集
子句集就是合取范式的各个部分组成的集合:
子句的性质
子句集S的不可满足性:对于任意论域中的任意一个解释,S中的子句不能同时取得真值T。
定理 设有谓词公式F,其子句集为S,则F不可满足的充要条件是S不可满足。
因为子句是从合取范式来的,只要一个子句永假,整个谓词公式就永假。
消解推理
设
例:
最一般合一(求法见上一篇):
归结式:
若某个子句
定理 若
推论 设
如果一个东西的逻辑结论为假,那它本身也假。
但是
推论 设
消解反演求解
用已知公式集
得到如下公式集:
化为子句集
应用归结原理对子句集S中的子句进行归结,并把每次归结得到的归结式都并入S中。如此反复进行,若出现了空子句,则停止归结,此时就证明了Q为真。
例:
求证:
证明:首先把
归结:
归结得到:
归结得到:
出现空子句,停止归结,证毕。
现实例子
设
用
三个人有真有假
如果一个为真,另外俩一定至少有个假的;一个为假,另外俩一定至少有个真的。
以上推出的子句集:
要证明
(1)和(7)得到
(2)和(9)得到
(8)和(10)得到
证毕,
在消解反演中,并不一定要用到全部的子句,只要能得到NIL他就是对的。
归结法的性质
归结法是仅有一条推理规则的推理方法;
归结法是完备的,即对于正确的逻辑公式,使用该方法可以在有限步内得到结论;
当不知公式是否为恒真时,归结原理不能得到任何结论(半可判定)。
归结过程的控制策略
目的是解决归结法知识爆炸的问题,使归结点尽量少,删除不必要的子句,给出控制策略,以便仅选择合适的子句对其做归结,避免多余的、不必要的归结式出现。
控制策略的方法
删除策略=>完备
归类:设有两个子句
若对
i
这里虽然
也就是不断地用小的来代表大的,缩减问题规模。
采用支撑集<=>完备
支撑集:设有不可满足子句集
采用支撑集策略时,从开始到得到空子句的整个归结过程中,只选取不同时属于
如果没有这样的限制,归结可能在
例
知识库
其中
得到空子句。
语义归结<=>完备
语义归结策略是将子句
还是用上边的子句集:
利用一个模型
子句集中前三句都能满足
得到的
满足
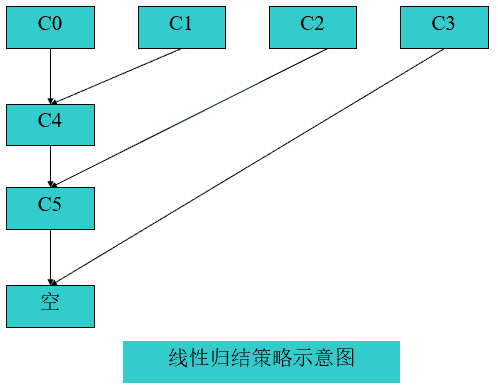
线性归结<=>完备
线性归结策略首先从子句集中选取一个称作顶子句的子句
单元归结=>完备
单元归结策略要求在归结过程中,每次归结都有一个子句是单元子句(只含一个文字的子句)或单元因子。显而易见,词中方法可以简单地削去另一个非单子句中的一个因子,使其长度减少,构成简单化,归结效率较高。
单元归结策略要求在归结过程中,每次归结都有一个子句是单元子句(只含一个文字的子句)或单元因子。显而易见,词中方法可以简单地削去另一个非单子句中的一个因子,使其长度减少,构成简单化,归结效率较高。
输入归结=>完备
与单元归结策略相似,输入归结策略要求在归结过程中,每一次归结的两个子句中必须有一个是S的原始子句。这样可以避免归结出的不必要的新子句加入归结,造成恶性循环。可以减少不必要的归结次数。
自动定理证明——Herbrand定理
要解决的问题
一阶逻辑公式的永真性(永假性)的判定是否能在有限步内完成?
定理思想
寻找一个已给的公式是真的解释。然而,如果所给定的公式的确是永假的,就没有这样的解释存在,并且算法在有限步内停止。
H域
因为量词是任意的,所讨论的个体变量域
称为
例如,求出如下子句集的
首先把子句集中的常量放入
之后按上述公式算出后边的
关于f的参数
以此类推,
原子集
即把
上例中的原子集为:
一旦原子集内真值确定好,则
H解释
谓词公式
定理1
设
定理2
子句集
定理3
子句集
基例
例如子句集:
它的
选定子句:
用
用
用
这些替换都是基例,所有的基例共同构成基例集。
若一个子句为假,则此解释为假;一般来说,论域
语义树
是原子集中所有元素逐层添加的一棵二叉树。将元素的是与非分别标记在两侧的分枝上。一般情况**
例如子句集:
它的原子集是:
按定义画出语义树:
即为每一个原子集中元素的真假取值都创建一个分支。
如果语义树某个分支进行到某个节点之后,已经能够确定公式为假,则这个点称为失败点,例如本例中标红的都是失败点:
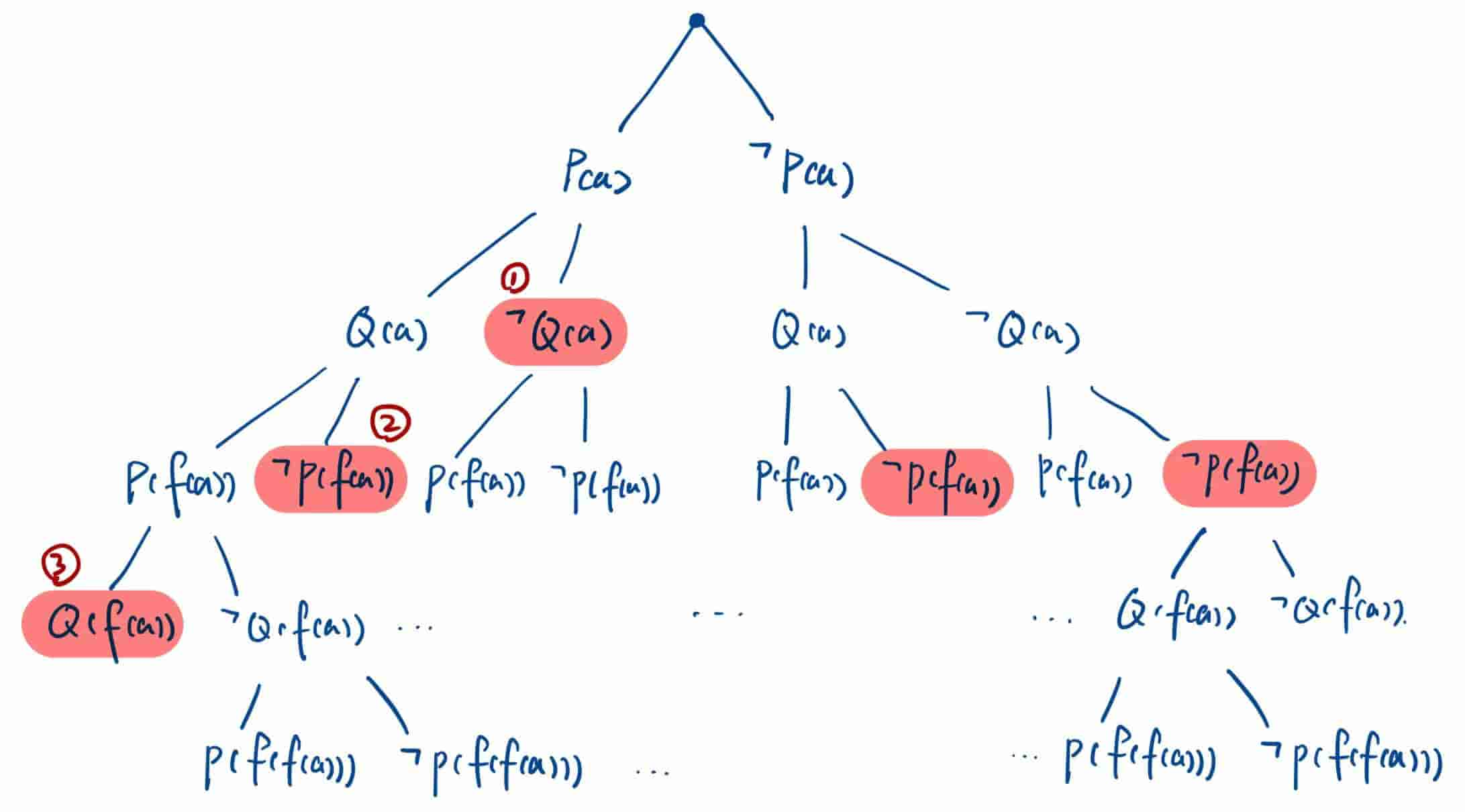
其中,①违反了
②违反了
如果
Herbrand定理
子句集
