搜索问题

关键问题是如何利用知识，尽可能有效地找到问题的解或最优解。

回溯

概述

精髓在于尝试和递归回溯。

八皇后问题

八皇后问题就是说在棋盘上摆8个皇后让她们互相不处于对方的控制域内。本例中为了演示方便把搜索空间减小为一个$4\times 4$的棋盘，变成四皇后问题。。

尝试

从坐标$(1,1)$开始试。当第一个皇后摆在棋盘$(1,1)$上时，她的控制域如下：

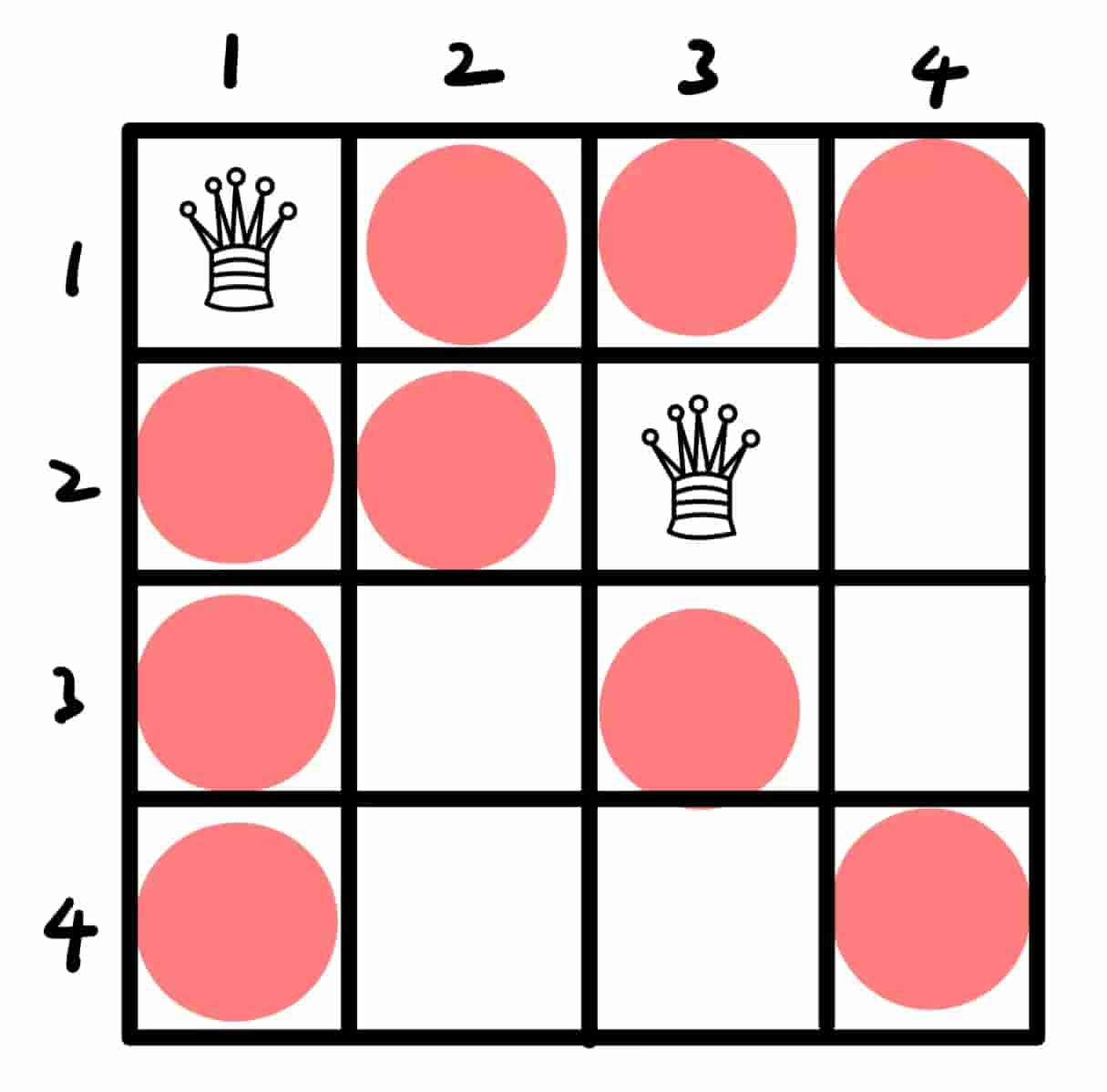
这时候从控制域外找第一个可以摆的地方，也就是$(3,2)$摆第二个皇后。摆上之后她们俩的控制域如下：

这时候就剩一个位置了，显然是摆不下四个皇后的。那就说明这一步摆法不行，也就是要么第一个皇后摆得有问题，要么第二个有问题。

回溯

先按顺序回溯到第二个皇后那里，换个地方摆：

发现还是不行。事实上我们尝试了把第二个皇后放在所有能摆的位置，最后都摆不下四个皇后。所以就可以认为是第一个皇后有问题。那就尝试把第一个皇后换个地方，换到第二个她能摆的地方：

之后依次尝试后几个皇后能摆的位置：

be636c8febfe683e5faf576cf18f59e

这次很幸运，所有位置都只尝试了一次就完成了这个问题。

算法表述

回溯的过程可以表达为一棵搜索树，目标是找到当前状态到目标状态的路径：

而前边提到的递归思想，就是说这棵树每往下搜索一层，就会开一棵子树，而这棵子树也有当前状态和一个全局唯一的目标状态。那么也可以使用这个算法。

但是简单的不加限制的回溯有可能产生死循环或深度过深。具体可以通过限制深度和记录初始状态到当前状态的路径来解决，如果在路径中发现了循环就回到开启循环的点，放弃这个带循环的子树去搜下一个叶子。

图搜索

回溯搜索只保留从初始状态到当前状态的一条路径，而图搜索保留所有已经搜索过的路径。

基本概念

路径的耗散值

一条路径的耗散值等于连接这条路径各节点间所有耗散值的总和。用$C(n_i,n_j)$表示从$n_i$到$n_j$的耗散值。相邻节点间的耗散值为1。

扩展一个节点

生成出该节点的所有后继节点，并给出它们之间的耗散值。这一过程称为“扩展一个节点”。

一般图搜索算法

按顺序搜索所有节点，如果不是目标就扩展。

修改指针

一个节点可能属于不同的路径，也有可能有很多可能的父节点。当一个节点的父节点需要更新时，就需要修改父节点指针。

无信息图搜索

BFS；DFS。

A算法(启发式搜索)

概述

利用知识来引导搜索，减少搜索范围。

启发信息强度

启发信息越强，越能降低搜索工作量，但可能导致找不到最优解。启发信息越弱，越会导致工作量加大，极限情况下变为非启发式（盲目）搜索，但有可能找到最优解。目标是在保证找到最优解的情况下尽量减少搜索复杂度。

基本思想

定义一个评价函数$f$，对当前的搜索状态进行评估，找出一个最有希望的节点来扩展。

评价函数

评价函数：

$$f(n)=g(n)+h(n)$$

其中$h(n)$是启发函数。

符号意义

$g^{\ast }(n)$：从$s$到$n$的最小耗散值（从开始到当前节点）；

$h^{\ast }(n)$：从$n$到$g$的最小耗散值（从当前节点到目标）；

$f^{\ast }(n)=h^{\ast }(n)+g^{\ast }(n)$：从开始经过当前节点到目标的最小耗散；

$f^{\ast }(n),g^{\ast }(n),h^{\ast }(n)$分别是$f(n),g(n),h(n)$的最佳估计值。

算法表述

A算法的伪代码和A*算法完全一样，只是A*带有启发函数：

$$f^{\ast }(n)=g^{\ast }(n)+h^{\ast }(n)$$

而A算法没有启发函数，它只算实际距离：

$$f(n)=g(n)+h(n)$$

i

A*的启发函数是对距离（代价）的一种估计方式。这个估计方式可以随意调整，如果把它设为实际距离，那么A*退化为A。

由于我先学的A*，所以这里写得比较简略。关于A*算法参考这篇文章，其中有详细的算法描述。

博弈树搜索

完全信息博弈

1. 双人博弈，对垒双方轮流走；
2. 信息完备，对垒双方得到的信息一样（斗地主、麻将、21点等不算完全博弈问题）；
3. 零和，即对一方有利的棋，对另一方肯定是不利的。对弈的结果是一方输，另一方赢；或者双方和棋，即结果零和。

博弈树

两种节点

MAX（极大节点），求极大值，选最大的；

MIN（极小节点），求极小值，选最小的。

极大极小搜索方法

这部分参考这篇文章。

评价函数

首先假定，有一个评价函数可以对所有的棋局进行评估。当评价函数值大于0时，表示棋局对我方有利，对对方不利。当评价函数小于0时，表示棋局对我方不利，对对方有利。

搜索过程

对于一棵博弈树：

其中所有的叶子都是最终的棋局状态。搜索原则是，每一层的取值都是它所有儿子节点的最大/最小值，具体是最大还是最小取决于这个节点是MAX还是MIN（如果是MAX其实就是我方走的步，否则反之）。

这个例子中$A,B,C$的取值都是它们儿子节点中的最小值：

而由于$s$是MAX节点，它应该取它所有儿子节点$A,B,C$的最大值，得到$s$的值后可以根据取值找到搜索路径：

极小极大过程是一种假定对手每次回应都正确（对手超级聪明，他每次都能选择最利于自己的走法）的情况下，如何从中找出对我方最有利的走步的搜索方法。

存在的问题

把搜索树的生成和估值两个过程分开进行，导致效率低（必须先有完整的树才能给节点赋值）。

如果把生成和倒推估值结合起来，根据一定的条件判定，可以修剪掉一些无用的分支。

α-β 剪枝

这部分参考了这个视频。

在min-max方法中，根据节点的类型是min还是max来决定是选最大值还是最小值。用max节点举例，其中隐含的思路是，父亲节点的取值开始时是$-\text{infin}$，每遍历一个子节点就决定一次是否向上更新自己的取值：

对于min节点，搜索则是一个不断尝试降低自己值的过程。所有的min节点上边都会有一个max节点，想取最大值。当一个min节点搜到一半就已然不可能满足其上方的max节点的要求时，它剩下的部分就没必要再搜了。

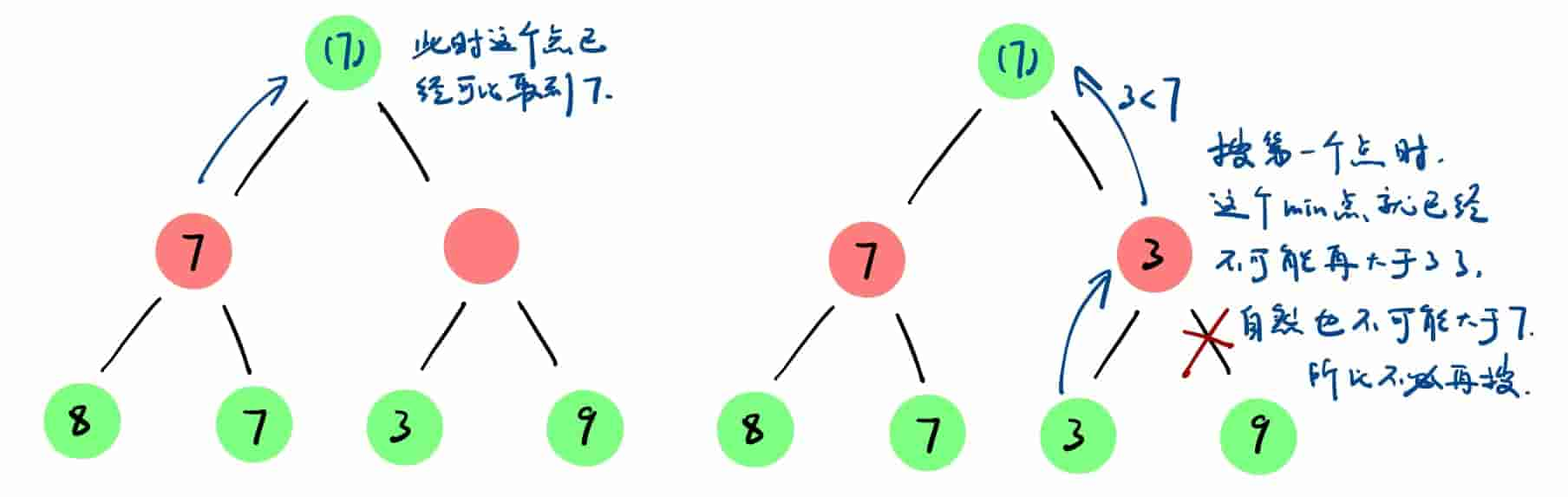
上图中右边的min节点首先搜到一个3，已经小于了其上方max节点确定可以取的值7。这个min节点后边无论搜到更小的或者更大的，对大局已经没有意义了，所以后边的一切子节点都可以直接剪掉。

按这种思想继续搜下去：

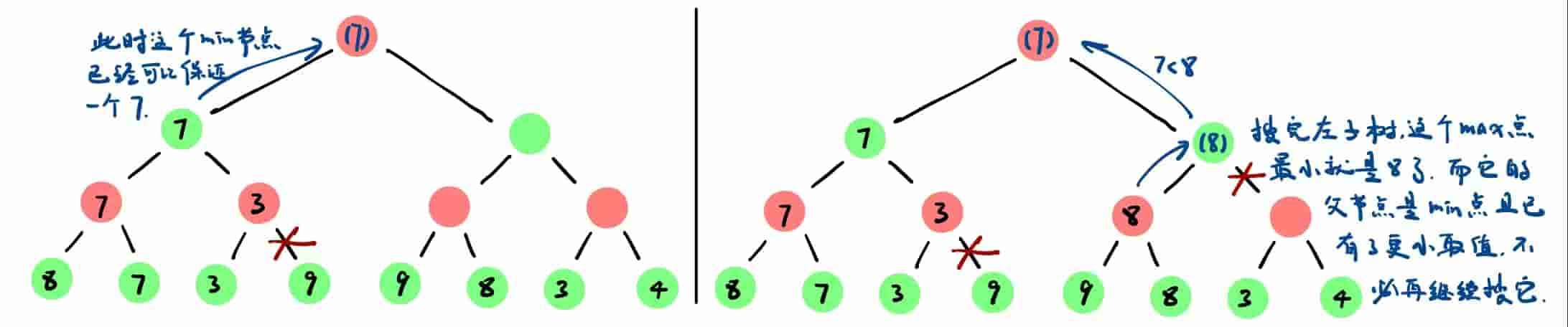
直到搜到根节点。

i

节点每更新一次值，都要看一眼父亲节点并作比较，看看是否还有必要继续搜。