7.Permutation group

Overview

Review the definition of symmetry group:

Let $A$ be an arbitrary set. $S_A=\{f\mid f\text{ is a permutation on }A\}$. The group formed by the composition of such permutations is called the symmetric group on $A$. -

Why is it called a symmetric group? This is because such groups describe the symmetry of objects. - In nature and real life, many objects have symmetry, such as isosceles triangles, squares, and regular polyhedra in geometric shapes. The symmetry of these shapes can be described as a transformation in the plane or space where the image of the shape coincides with itself.

For example:

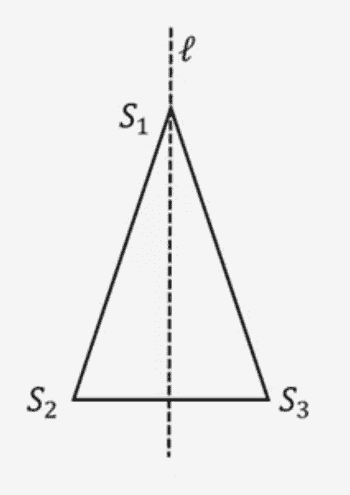
For the isosceles triangle below, if it is flipped along the axis of symmetry, there are two types of transformations:

Identity transformation: $I(S_1)=S_1,I(S_2)=S_2,I(S_3)=S_3$

Reflection transformation: $\tau (S_1)=S_1,\tau (S_2)=S_3,\tau (S_3)=S_2$

Thus, $<S_1,S_2,S_3,I,\tau >$​​ forms a subgroup of the symmetric group on three elements.

The roots of equations also have symmetry. For example, the two complex roots $x_1$ and $x_2$ of the quadratic equation $x^2+bx+c=0$ satisfy

$$x_1+x_2=-b,x_1{x}_2=c$$

Where is the symmetry reflected? Create a permutation $\sigma$ on $A=\{x_1,x_2\}$: $\sigma (x_1)=x_2,\sigma (x_2)=x_1$. Substituting this permutation into equation, we get

$$x_2+x_1=-b,x_2{x}_1=c$$

Both expressions are identical. This is the symmetry of the equation's roots.

Definition

Every subgroup of the symmetric group is called a transformation group on $A$.

When $|A|=n$, the symmetric group on $A$ is called the $n$-th symmetric group, denoted as $S_n$.

Any subgroup of $S_n$ is called an $n$-th permutation group.

A transformation group is actually a group composed of transformations, for example, if every element of a symmetry group is a transformation, then every element of its subgroup is also a transformation. However, not every subgroup of a group composed of transformations is a transformation group, because to satisfy closure, the elements of the group cannot change after the transformation. Then only the subgroups of the permutation group satisfy this requirement.

Transformation

When $S$ is a finite set with $|S|=n$, any permutation on $S$ is called an $n$-th permutation. For convenience, let $S=\{1,2,\dots ,n\}$, and a permutation $\sigma$ can be denoted as:

$$\sigma =\left(\begin{array}{cccc}1& 2& \cdots & n\\ \sigma (1)& \sigma (2)& \cdots & \sigma (n)\end{array}\right)$$

Since $\sigma$ is a bijection on $S$, $\sigma (1)\sigma (2)\cdots \sigma (n)$ is a permutation of the elements $1,2,\cdots ,n$. Therefore, the order of the symmetric group $S_n$, which is the $n$-th symmetric group, is $n!$. The composition of any two permutations in $S_n$ can be called the product of permutations. For example, in $S_4$,

$$\sigma =\left(\begin{array}{cccc}1& 2& 3& 4\\ 2& 3& 4& 1\end{array}\right),\tau =\left(\begin{array}{cccc}1& 2& 3& 4\\ 3& 2& 1& 4\end{array}\right)$$

Thus, $$ \sigma \tau = \begin{pmatrix} 1 & 2 & 3 & 4 \ 4 & 3 & 2 & 1 \end{pmatrix}, \quad \tau \sigma = \begin{pmatrix} 1 & 2 & 3 & 4 \ 4 & 2 & 3 & 1 \end{pmatrix}. $$​ (This uses right-composition here.)

See this article for details.

Cycles and transpositions

A permutation can be expressed as a product of cycles or transpositions.

Let $r$ be an $n$-th permutation. If it satisfies:

(1) $r(a_1)=a_2,r(a_2)=a_3,\dots ,r(a_l)=a_1$

(2) $r(a)=a,a\ne a_i(i=1,2,\dots ,l)$

Then $r$ is called a cycle of length $l$, denoted as $r=(a_1,a_2,\dots ,a_l)$. A cycle of length $2$ is called a transposition.

For example, in $S_6$,

$$\sigma =\left(\begin{array}{cccccc}1& 2& 3& 4& 5& 6\\ 3& 2& 4& 5& 1& 6\end{array}\right)=(1345),\tau =\left(\begin{array}{cccccc}1& 2& 3& 4& 5& 6\\ 1& 5& 3& 4& 2& 6\end{array}\right)=(25)$$

So $\sigma$ is a cycle of length $4$​, not a transposition.

Decomposition of permutation

Find the cycle decomposition and a transposition decomposition of the following permutations.

$$\sigma =\left(\begin{array}{ccccccc}1& 2& 3& 4& 5& 6& 7\\ 3& 7& 5& 2& 1& 6& 4\end{array}\right)$$$$\sigma =\left(\begin{array}{ccccccc}1& 2& 3& 4& 5& 6& 7\\ 3& 7& 5& 2& 1& 6& 4\end{array}\right)=(135)(274)(6)$$$$=(135)(274)=(13)(15)(27)(24)$$

The 6 is called the fixed point and can be omitted in the alternate resolution.

Parity of permutations

Let $\sigma$ be any $n$-permutation. If $\sigma$ can be decomposed into an even number of transpositions, then $\sigma$​ is called an even permutation; otherwise, it is called an odd permutation.

In other words, what you get by swapping an odd number of times is an odd permutation.

The product of two even permutations is still an even permutation, the product of two odd permutations is also an even permutation, and the product of an even permutation and an odd permutation is an odd permutation.

The number of odd permutations in the symmetric group $S_n$ accounts for half, which is $\frac{n!}{2}$.

All even permutations in $S_n$ form a subgroup, called the n-th alternating group, denoted as $A_n$.

The identity element of $S_n$ (which is the identity transformation, denoted as $(1)$) is also an even permutation.

Type of permutation

Let $\sigma$ be any $n$-permutation. If the cycle decomposition of $\sigma$ consists of ${\lambda }_1$ 1-cycles, ${\lambda }_2$ 2-cycles, ..., ${\lambda }_n$ $n$-cycles, then $\sigma$ is called a permutation of type $1^{{\lambda }_1}{2}^{{\lambda }_2}\dots n^{{\lambda }_n}$, where $1\cdot {\lambda }_1+2\cdot {\lambda }_2+\dots +n\cdot {\lambda }_n=n$.

For example, $(123)$ in $S_5$ is a permutation of type $1^2{3}^1$ (because there are also two 1-permutation: $(123)(4)(5)$), $(12345)$ is a permutation of type $5^1$, and $(12)(34)$ is a permutation of type $1^1{2}^2$. It can be proven that, in $S_n$, the number of permutations of type $1^{{\lambda }_1}{2}^{{\lambda }_2}\dots n^{{\lambda }_n}$ is

$$\frac{n!}{1^{{\lambda }_1}{2}^{{\lambda }_2}\dots n^{{\lambda }_n}{\lambda }_1!{\lambda }_2!\dots {\lambda }_n!}$$

dihedral group

Consider the rotations or reflections of a regular $n$-gonn in three-dimensional space that keep the relative positions of its vertices unchanged:

Each rotation or reflection corresponds to a permutation of its set of vertices. The product of two permutations is a rotation or reflection followed by another rotation or reflection. The inverse of a rotation or reflection is its opposite rotation or reflection.

All rotations or reflections form a group, which is a subgroup of the symmetric group $S_n$, also known as a permutation group, called the dihedral group, denoted as $D_n$.

Cayley's theorem

Let $G$ be a random group, then

(1) $G$​ is isomorphic to a transformation group.

(2) If $G$ is a finite group, then $G$​ is isomorphic to a permutation group.

Example:

Find the permutation group isomorphic to the Klein four-group. Solution: Given the Klein four-group $K=\{e,a,b,c\}$, according to Cayley's theorem, we have $G^{\prime }=\{f_g|g\in K,\mathrm{\forall }x\in K,f_g(x)=gx\}$ Thus,

$$\begin{gathered} f_e=\left(\begin{array}{cccc}e& a& b& c\\ e& a& b& c\end{array}\right)=(1), \\ {f}_a=\left(\begin{array}{cccc}e& a& b& c\\ a& e& c& b\end{array}\right)=(ea)(bc), \end{gathered}$$

The reason why $ab=c$ here is that there are only four elements in the set, and neither $a$ nor $b$ are identity elements, so the result can't be $a$ or $b$, let alone $e$, so the result can only be $c$. That is to say, any two elements in the Klein quaternion other than $e$ can only be equal to the third element.

$$\begin{gathered} f_b=\left(\begin{array}{cccc}e& a& b& c\\ b& c& e& a\end{array}\right)=(eb)(ac), \\ {f}_c=\left(\begin{array}{cccc}e& a& b& c\\ c& b& a& e\end{array}\right)=(ec)(ab) \end{gathered}$$

Using $\{1,2,3,4\}$ to replace $\{e,a,b,c\}$, we have $K\cong \{(1),(12)(34),(13)(24),(14)(23)\}$.